ГРАФЫ
Фигура образованная конечным набором точек плоскости и отрезков, соединяющих
некоторые из этих точек, называется графом (рис. 24.1, а). Точки
называются вершинами, а отрезки – ребрами графа.
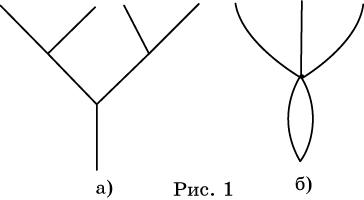
Граф называется связным, если любые две его вершины
можно соединить ломаной, состоящей из ребер графа.
Граф называется простым, если его
различные ребра не пересекаются.
Вместо отрезков в качестве ребер графов рассматриваются также кривые
линии на плоскости (рис. 1, б).
Примерами графов могут служить схемы метрополитена, железных и шоссейных
дорог, планы выставок и т.д.
Исторически сложилось так, что теория графов зародилась в ходе решения
головоломок двести с лишним лет назад.
Одной из таких задач-головоломок была задача о кёнигсбергских мостах,
которая привлекла к себе внимание Леонарда Эйлера (1707-1783), долгое время
жившего и работавшего в России (с 1727 по 1741 год и с 1766 до конца жизни).
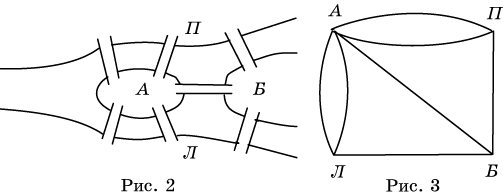
Задача. В г.
Кёнигсберге (ныне Калининград) было семь мостов через реку Прегель (рис. 2, где
Л - левый берег, П - правый берег, А и Б - острова). Задача заключалась в
следующем: можно ли, прогуливаясь по городу, пройти через каждый мост ровно
один раз?
Эта задача связана с другими головоломками, суть
которых заключалась в том, чтобы обвести контур некоторой фигуры, не отрывая
карандаша от бумаги и не обводя ни одной линии контура дважды, т.е.
"нарисовать одним росчерком". Такие контуры образуют так называемые уникурсальные
графы.
Задаче о кёнигсбергских мостах Л. Эйлер посвятил целое исследование,
которое в 1736 году было представлено в Петербургскую Академию наук.
На рисунке 3 изображен граф, соответствующий задаче о кёнигсбергских
мостах. Требуется выяснить, является ли этот граф уникурсальным.
Для этого Эйлер ввел понятие индекса вершины - число ребер графа,
сходящихся в данной вершине, и доказал, что имеет место следующая теорема.
Теорема. Для
уникурсального графа число вершин нечетного индекса равно нулю или двум.
Доказательство. Действительно,
если граф уникурсален, то у него есть начало и конец обхода. Если начало не
совпадает с концом, то начало и конец являются единственными вершинами
нечетного индекса. Остальные вершины имеют четный индекс, так как в каждую из
них мы входим и выходим из нее. Если начало совпадает с концом, то вершин с
нечетным индексом нет.
Приступим теперь к решению задачи о кёнигсбергских мостах. Определим
индексы вершин графа на рисунке 3. Вершина А имеет индекс 5, Б - 3, П - 3 и Л
- 3. Таким образом, мы имеем четыре вершины нечетного индекса, и, следовательно,
данный граф не является уникурсальным. Отсюда получаем, что во время прогулки
по городу нельзя пройти по каждому из семи мостов только один раз.
Исторические сведения
В 2007 году исполнилось 300 лет со дня рождения Леонарда Эйлера – одного из величайших математиков, работы
которого оказали решающее влияние на развитие многих современных разделов
математики. Л.Эйлер был действительным членом Петербургской Академии наук,
оказал большое влияние на развитие
отечественной математической школы и в деле подготовки кадров
ученых-математиков и педагогов в России. Поражает своими размерами научное
наследие ученого. При жизни им опубликовано 530 книг и статей, а сейчас их известно
уже более 800. Причем последние 12 лет своей жизни Эйлер тяжело болел, ослеп и,
несмотря на тяжелый недуг, продолжал работать и творить. Статистические
подсчеты показывают, что Эйлер в среднем делал одно открытие в неделю. Трудно
найти математическую проблему, которая не была бы затронута в произведениях
Эйлера. Все математики последующих поколений так или иначе учились у Эйлера, и
недаром известный французский ученый П.С.Лаплас сказал: "Читайте Эйлера,
он – учитель всех нас".
1. Нарисуйте графы, у
которых имеются вершины индексов 1, 2, 3 и 4.
2. Нарисуйте граф, в котором
каждая вершина имеет индекс, равный: а) двум; б) трем; в) четырем.
3. В графе 10 вершин, каждая из которых имеет индекс 3. Сколько у него
ребер? Нарисуйте такой граф.
4. В графе 5 вершин, каждая из которых имеет индекс 4. Сколько у него
ребер? Нарисуйте такой граф.
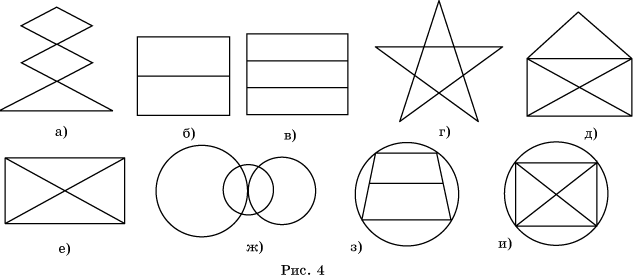
5. Определите, какие графы, изображенные на рисунке 4, являются
уникурсальными?
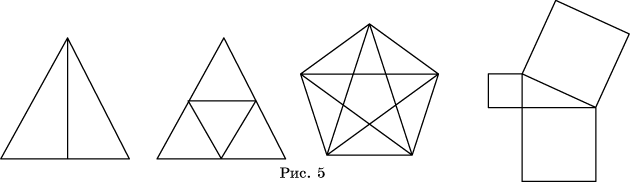
6.
Нарисуйте одним росчерком фигуры,
изображенные на рисунке 5.
7. Может ли граф иметь
только одну вершину нечетного индекса?
8. Докажите, что в любом графе сумма индексов всех его вершин - число
четное, равное удвоенному числу ребер графа. Выведите из этого, что число
вершин с нечетными индексами четно.
9. Докажите, что во всяком графе, ребрами которого являются отрезки,
найдутся, по крайней мере, две вершины одинакового индекса.
10.
Какое наименьшее число мостов в задаче о кёнигсбергских мостах придется пройти
дважды, чтобы пройти по каждому мосту?
11.
Докажите, что если в задаче о кёнигсбергских мостах добавить еще один мост в любом
месте реки Прегель, то полученный граф будет уникурсальным.
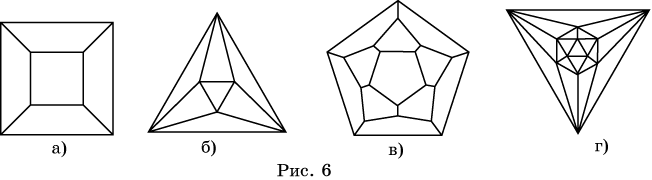
12.
Какое наименьшее число ребер придется обвести дважды, чтобы нарисовать, не
отрывая карандаша от бумаги, графы, изображенные на рисунке 6?
13. Докажите, что если у связного графа число вершин нечетного индекса
равно нулю или двум, то он является уникурсальным.
Еще
одной задачей-головоломкой, связанной с графами и с именем Эйлера, является
задача о трех домиках и трех колодцах.
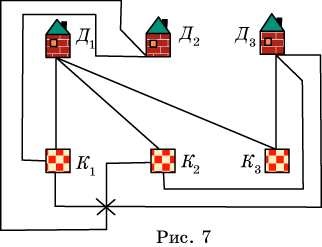
Задача. Три
соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от
каждого дома к каждому колодцу (рис. 7)?
Для решения этой задачи воспользуемся теоремой,
доказанной Леонардом Эйлером в 1752 году.
Теорема. Для произвольного связного простого графа на
плоскости имеет место равенство
В - Р
+ Г = 2, (*)
где В
- число вершин, Р - число ребер, Г - число областей, на которые граф разбивает
плоскость.
Доказательство.
Докажем, что равенство (*) не изменится, если какие-нибудь две соседние вершины
простого связного графа (рис. 8, а) стянуть в одну вместе с соединяющим их
ребром.
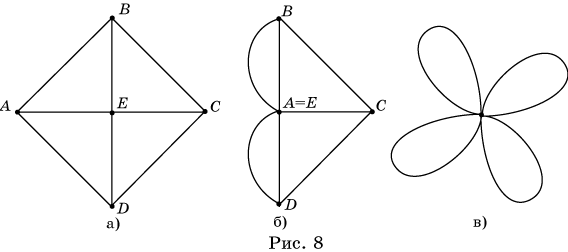
Действительно, после такого стягивания в новом графе (рис. 8, б) будет В – 1
вершина, Р – 1 ребро, а количество областей не изменится. Следовательно, имеем
(В –
1) - (Р – 1) + Г = В – Р + Г.
Будем последовательно
стягивать соседние вершины, пока не получим граф с одной вершиной (рис. 8, в).
Ребрами этого графа будут петли, а В – Р +
Г останется таким же, как и для исходного графа.
Уберем в
полученном графе одно ребро. При этом число вершин не измениться, число ребер
уменьшится на единицу, число областей также уменьшится на единицу.
Следовательно, В – Р + Г не
изменится. Будем последовательно убирать ребра графа, пока не останется одно
ребро в виде петли. Для такого графа В = 1,
Р = 1, Г = 2 и, следовательно, имеет место равенствоB - Р + Г= 2. Значит, оно имеет место и для исходного графа.
Приступим теперь к решению задачи о трех домиках и трех колодцах.
Решение.
Предположим, что это можно сделать. Отметим домики точками Д1, Д2,
Д3, а колодцы - точками К1, К2, К3
(рис. 7). Каждую точку-домик соединим с каждой точкой-колодцем. Получим девять
ребер, которые попарно не пересекаются.
Эти ребра образуют на плоскости связный простой граф. Поэтому для него
выполняется соотношение Эйлера В - Р + Г = 2, причем В = 6 и Р = 9.
Следовательно, Г = 5. Каждая из пяти областей имеет по крайней мере четыре
ребра, поскольку, по условию задачи, ни одна из дорожек не должна
непосредственно соединять два дома или два колодца. Так как каждое ребро лежит
входит в границу ровно двух областей, то количество ребер должно быть не
меньше (5∙4)/2 = 10, что противоречит условию, по которому их число равно
9. Полученное противоречие показывает, что ответ в задаче отрицателен - нельзя
провести непересекающиеся дорожки от каждого домика к каждому колодцу.
1. Связный
граф, не содержащий ни одной замкнутой ломаной, называется деревом. Докажите, что для любого дерева, имеющего В
вершин и Р ребер, справедливо соотношение: В - Р = 1. Приведите примеры
графов, для которых В – Р ![]() 1.
1.
2. Граф, не содержащий ни одной замкнутой ломаной, называется лесом.
Пусть лес состоит из n деревьев и имеет В вершин и Р
ребер. Чему равно В - Р?
3.
Нарисуйте графы, для которых В - Р равно: а) 0; б) 1; в) 2; г) -1; д) -2.
4. Докажите, что для
произвольного разбиения четырехугольника на четырехугольники выполняется
равенство В – Г = 3.
5. Два соседа имеют: а) три общих колодца; б) четыре
общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к
каждому колодцу?
6. Три
соседа имеют: а) два общих колодца; б) четыре общих колодца. Можно ли провести
непересекающиеся дорожки от каждого дома к каждому колодцу?
7.
Четыре соседа имеют четыре общих колодца. Можно ли провести непересекающиеся
дорожки от домиков к колодцам так, чтобы каждый домик был соединен ровно с
тремя колодцами, и каждый колодец – с тремя домиками?
8.
Можно ли пять точек на плоскости соединить непересекающимися линиями так, чтобы
каждая точка была соединена с каждой?
9.
Можно ли шесть точек на плоскости соединить непересекающимися линиями так,
чтобы каждая точка была соединена ровно с: а) тремя; б) четырьмя; в) пятью
другими?
10. Внутри n -
угольника взяты m точек.
Эти точки и вершины многоугольника соединены отрезками так, что исходный
многоугольник разбивается на треугольники. Докажите, что при этом число
треугольников равно n + 2m - 2.
11.
Многоугольник разбит на конечное число многоугольников так, что в каждой
вершине сходится три ребра. Сколько при этом имеется вершин и граней, если
число ребер равно: а) 6; б) 12; в) 15? Нарисуйте такие разбиения.
12. Докажите, что для любого разбиения n-угольника на m-угольники выполняется
равенство 2В + (2 – m)Г = n + 2.
Литература
1. Адамар Ж. Элементарная геометрия. Часть II.
Стереометрия. – М.: Учпедгиз, 1938.
2. Долбилин Н.П. Жемчужины теории
многогранников. – М.: МЦНМО, 2000, с.27-31.
3. Перепелкин Д.И. Курс элементарной геометрии.
Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949, с.273 (с.276 -
§ 4).
4. Смирнова И.М. В мире многогранников. – М.:
Просвещение, 1995.
5. Шклярский Д.О., Ченцов Н.Н., Яглом И.М.
Избранные задачи и теоремы элементарной математики. Часть 3. Геометрия
(Стереометрия). – М.; 1954, с.15, с.18 /Библиотека математического кружка,
выпуск 3.
6. Энциклопедия элементарной математики. Книга
IV. Геометрия. - М.: 1963.
7. Яглом И.М., Болтянский В.Г. Выпуклые фигуры.
– М.-Л.; 1951 /Библиотека математического кружка, выпуск 4.