ИЗМЕРЕНИЕ ДВУГРАННЫХ И МНОГОГРАННЫХ УГЛОВ

         Двугранные и многогранные углы входят в новые стандарты по математике как базового, так и профильного уровня обучения в старших классов. Однако задачам на вычисление этих углов обычно не уделяется должного внимание. В то же время решение таких задач способствует выработке необходимых вычислительных навыков, повторяет различные планиметрические формулы и соотношения, развивает пространственные представления учащихся.

Здесь мы рассмотрим вопрос об измерении двугранных и многогранных углов. Предлагаемый материал и задачи могут быть использованы на профильном уровне при изучении темы «Правильные многогранники», при проведении элективных курсов, подготовке учащихся к решению олимпиадных задач и задач вступительных экзаменов по математике в вузы.

Начнем с двугранных углов. Двугранный угол является пространственным аналогом угла на плоскости. Напомним, что углом на плоскости называется фигура, образованная двумя лучами этой плоскости с общей вершиной и частью плоскости, ограниченной этими лучами. Будем считать аналогом точки на плоскости прямую в пространстве и аналогом луча на плоскости полуплоскость в пространстве. Тогда, по этой аналогии, двугранным углом в пространстве называют фигуру (рис. 1), образованную двумя полуплоскостями, с общей ограничивающей их прямой, и частью пространства, ограниченной этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла.

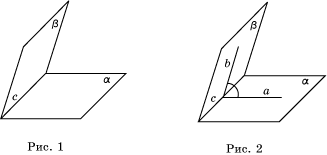
Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).

         Величиной двугранного угла называется величина его линейного уг­ла.

         В школьном курсе геометрии доказывается, что величина линейного угла не зависит от выбора плоскости, перпендикулярной его ребру.

         Найдем двугранные углы правильных многогранников.

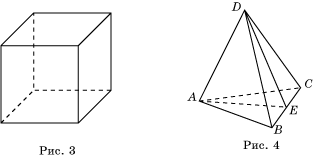
         Ясно, что двугранные углы j_куб куба (рис. 3) равны 90°_. Рассмотрим правильный тетраэдр ABCD с ребром 1 (рис. 4). Из вершин A и  D опустим перпендикуляры AE и DE на ребро BC. Для нахождения двугранного угла j_тет = ÐAED воспользуемся теоремой косинусов, примененной к треугольнику ADE, в котором AD = 1, AE = DE = . Имеем равенство 1 = +- 2cosj_тет. Откуда cosj_тет = , j_тет »70°30'.

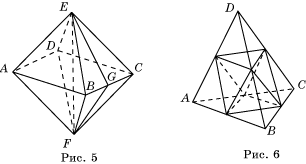
         Вычислим косинус двугранного угла октаэдра с ребром 1. Для этого из вершин E и F (рис. 5) опустим перпендикуляры EG и FG на ребро BC. EG = FG =. Четырехугольник AECF – квадрат со стороной 1 и, следовательно, EF = . По теореме косинусов имеем 2 =  +  - 2cosj_окт. Откуда cos j_окт = - ,  j_окт »109°30'.

         Заметим, что двугранные углы тетраэдра и октаэдра в сумме составляют 180°. Этот факт можно вывести и не вычисляя двугранных углов, а используя то, что середины ребер правильного тетраэдра являются вершинами октаэдра (рис. 6).

         Вычислим косинус двугранного угла икосаэдра с ребром 1. Для этого из A и C опустим перпендикуляры AG и CG на ребро BF (рис. 7). AG = CG =. AC является диагональю правильного пятиугольника ABCDE с ребром 1 и, следовательно, AC = 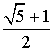. По теореме косинусов, имеем 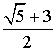=  +  - 2cosj_ико. Откуда cosj_ико = -, j_ико »138°11'.

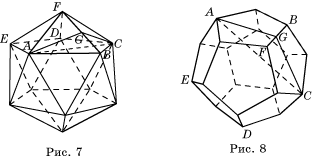
         Вычислим косинус двугранного угла додекаэдра с ребром 1. Для этого из вершин A и C опустим перпендикуляры AG  и CG на ребро BF (рис. 8). AG = CG = 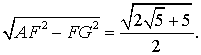 AC является диагональю правильного пятиугольника ABCDE с ребром 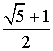. Поэтому, AC =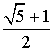 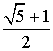=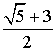. По теореме косинусов, имеем 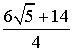=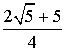+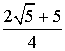-2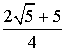cosj_дод. Откуда cosj_дод = -, j_дод »116°34'.

         Из приведенных вычислений, в частности следует, что из равных правильных многогранников, отличных от куба, нельзя составить пространственный паркет (заполнить все пространство). Действительно, если бы, такое заполнение пространства существовало, то сумма двугранных углов правильных многогранников с общим ребром должна была быть равна 360°. Следовательно, величина двугранного угла правильного многогранника могла бы быть получена делением 360° на натуральное число. Непосредственно видно, что из правильных многогранников этим свойством обладает только куб.

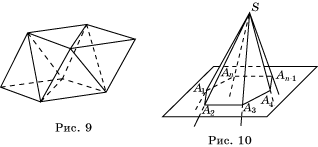
         Пространственный паркет можно составить используя тетраэдр и октаэдр. Для этого сначала нужно к двум противоположным граням октаэдра приставить тетраэдры (рис. 9). В результате получим параллелепипед, гранями которого являются ромбы. А уже затем из этих параллелепипедов составить пространственный паркет.

         Перейдем теперь к многогранным углам. Многогранный угол является пространственным аналогом многоугольника. Напомним, что многоугольником на плоскости называется фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью. Будем считать аналогом точки на плоскости луч в пространстве и аналогом отрезка на плоскости плоский угол в пространстве. Тогда аналогом простой замкнутой ломаной на плоскости является поверхность, образованная конечным набором плоских углов A₁SA₂, A₂SA₃, …, A_n-1SA_n, A_nSA₁ с общей вершиной S (рис. 10), в которых соседние углы не имеют общий точек, кроме точек общего луча, а несоседние углы не имеют общих точек, кроме общей вершины. Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется вершиной многогранного угла. Лучи SA₁, …, SA_n называются ребрами многогранного угла, а сами плоские углы A₁SA₂, A₂SA₃, …, A_n-1SA_n, A_nSA₁ – гранями многогранного угла. 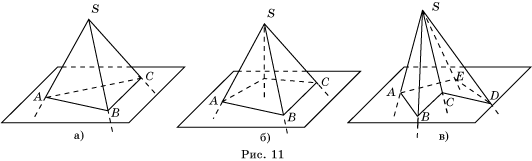Многогранный угол обозначается буквами SA₁…A_n, указывающими вершину и точки на его ребрах. В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными (рис. 11) и т. д.

Рассмотрим вопрос об измерении многогранных углов. Поскольку градусная величина развернутого двугранного угла измеряется градусной величиной соответствующего линейного угла и равна 180°, то будем считать, что градусная величина всего пространства, которое состоит из двух развернутых двугранных углов, равна 360°. Величина многогранного угла, выраженная в градусах, показывает какую часть пространства занимает данный многогранный угол. Например, трехгранный угол куба занимает одну восьмую часть пространства и, значит, его градусная величина равна 360°= 45°. Трехгранный угол в правильной n-угольной призме равен половине двугранного угла при боковом ребре. Учитывая, что этот двугранный угол равен  , получаем, что трехгранный угол призмы равен 

В школьном курсе геометрии доказывается, что для выпуклого n-угольника имеет место следующая формула для суммы его углов

Здесь мы получим пространственный аналог этой формулы для выпуклых многогранных углов.

Начнем с трехгранного угла. Опишем около его вершины S единичную сферу и обозначим точки пересечения ребер трехгранного угла с этой сферой  A, B, C (рис. 12).

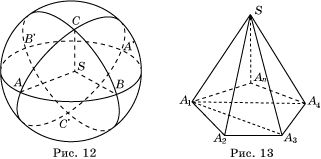
Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360°  плюс учетверенная величина трехгранного угла, или

(1)    ÐSAB +ÐSB + ÐSC = 180° + 2ÐSABC.

Пусть теперь SA₁…A_n – выпуклый n-гранный угол (рис. 13). Разбивая его на трехгранные углы, проведением диагоналей A₁A₃, …, A₁A_n-1 и применяя к ним полученную формулу, будем иметь

(2)    ÐSA₁ + … +ÐSA_n= 180° (n – 2) + 2ÐSA₁…A_n,

Используя эти формулы, вычислим многогранные углы y_куб, y_тет, y_окт, y_ико, y_дод, правильных многогранников. Имеем

y_куб = 45°; y_тет = j_тет - 90°»15°45'; y_окт = 2j_окт - 180° » 38°56';

y_ико = j_ико - 270°»75°28'; y_дод = j_дод - 90°»84°51'.

         Найдем двугранные и многогранные углы ромбододекаэдра – многогранника, гранями которого являются двенадцать ромбов (рис. 14).

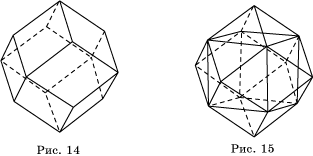
         Воспользуемся тем, что ромбододекаэдр может быть получен из двух равных кубов. А именно, разобьем один из двух кубов на правильные четырехугольные пирамиды, основаниями которых служат грани куба, а вершинами – центр куба. Поставим эти пирамиды основаниями на грани другого куба (рис. 15). Получим ромбододекаэдр.

         Из этого построения, в частности следует, что равными ромбододекаэдрами можно заполнить все пространство (составить пространственный паркет). Для этого сначала заполним пространство равными кубами, закрашенными в черный и белый цвета в шахматном порядке. Затем белые кубы разобьем на правильные четырехугольные пирамиды и присоединим их к черным кубам. Получим искомое заполнение пространства ромбододекаэдрами. При этом в каждой вершине сходится или шесть равных четырехгранных углов, или четыре равных трехгранных углов ромбододекаэдров.

         Таким образом, величина четырехгранного угла ромбододекаэдра равна 60°, а величина трехгранного угла ромбододекаэдра равна 90°.

         Двугранные углы ромбододекаэдра находятся из приведенной выше формулы (3) и равны 120°.

Используя теорему Эйлера о числе вершин ребер и граней выпуклого многогранника (В–Р+Г=2), выведем формулу, связывающую суммы двугранных и многогранных углов выпуклого многогранника.

Пусть  n₁, ..., n_в - количества ребер, сходящихся в вершинах данного многогранника. Тогда, суммируя соответствующие равенства по всем вершинам многогранника, и учитывая, что при этом каждый двугранный угол считается дважды, получим равенство

2S₂ = 180°(n₁ – 2) + ... + 180°(n_в – 2) + 2S,

где S₂, S - суммы двугранных и многогранных углов данного многогранника.

Заметим, что n₁ + ... + n_в = 2Р. Следовательно, будем иметь равенство

S₂ = 180°(Р – В) + S,

или, окончательно, используя соотношение Эйлера, В – Р + Г = 2, получаем

S₂ = 180°(Г – 2) + S.

Многогранные углы можно измерять и числами. Действительно, тремстам шестидесяти градусам всего пространства соответствует число 2p, равное половине площади единичной сферы. Поэтому численной величиной многогранного угла считают половину площади сферического многоугольника, высекаемого многогранным углом из единичной сферы с центром в вершине данного многогранного угла.

Например, численная величина трехгранного угла куба будет равна .

         Переходя от градусов к числам  в формулах 1 и 2, связывающих двугранные углы трехгранного и многогранного углов, будем иметь

(3)       ÐSAB +ÐSB + ÐSC = p + 2ÐSABC.

(4)         ÐSA₁ + … +ÐSA_n=p(n – 2) + 2ÐSA₁…A_n.

Заменяя в этих формулах величины трехгранного и многогранного углов на площади сферических треугольника и многоугольника, соответственно, получим формулы для площадей сферического треугольника ABC и многоугольника A₁…A_n.

(5)       S(ABC) = ÐSA +ÐSB + ÐSC –  p.

(6)        S(A₁…A_n) = ÐSA₁ + … +ÐSA_n – p(n – 2).

 

Задачи для самостоятельного решения

1. Чему равен трехгранный угол, образованный диагоналями граней куба, выходящими из одной вершины?

2. В правильном тетраэдре ABCD точка O – центр описанной сферы. Найдите трехгранный угол OABC и двугранные углы OA, OB, OC.

3. В правильной треугольной пирамиде боковое ребро равно 1, сторона основания . Найдите трехгранный угол при вершине и двугранные углы при боковых ребрах этой пирамиды.

4. В правильной треугольной пирамиде сторона основания равна 1, высота . Найдите трехгранный угол при вершине и двугранные углы при боковых ребрах этой пирамиды.

5. В правильной четырехугольной пирамиде сторона основания и боковое ребро равно 1. Чему равны двугранные и трехгранные углы при основании?

6. В правильной четырехугольной пирамиде сторона основания равна 2 см, высота 1 см. Чему равен многогранный угол при вершине этой пирамиды?

7. В правильной пятиугольной пирамиде сторона основания и боковое ребро равны 1. Чему равен пятигранный угол при вершине этой пирамиды?

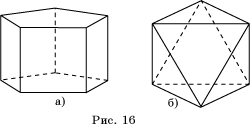
8. Найдите двугранные и многогранные углы: а) правильной пятиугольной призмы (рис. 16, а); б) правильной треугольной антипризмы (рис. 16, б).

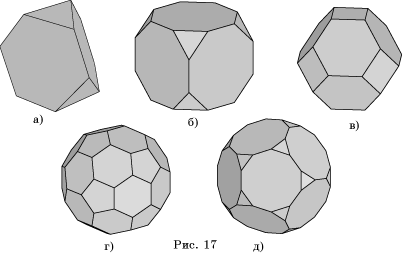
9. Найдите двугранные и многогранные углы: а) усеченного тетраэдра (рис. 17, а); б) усеченного куба (рис. 17, б); в) усеченного октаэдра (рис. 17, в); г) усеченного икосаэдра (рис. 17, г); д) усеченного додекаэдра (рис. 17, д).

10. Докажите, что из равных усеченных октаэдров можно составить пространственный паркет.

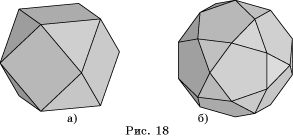
11. Найдите двугранные и многогранные углы: а) кубооктаэдра (рис. 18, а); б) икосододекаэдра (рис. 18, б).

12. Найдите величины невыпуклых многогранных углов многогранников, изображенных на рисунке 19, а-в.

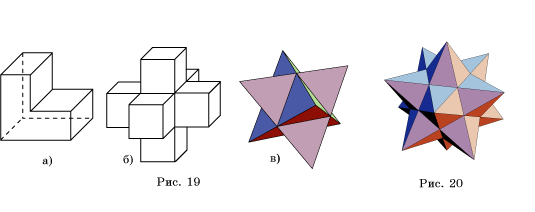
13. Найдите двугранные и многогранные углы малого звездчатого додекаэдра (рис. 20), получающегося из додекаэдра продолжением его ребер.

14. Верна ли формула (2) для невыпуклых многогранных углов? Почему?

15. Найдите площадь части сферы с центром в вершине единичного куба и радиусом 1, заключенной внутри этого куба.

16. В правильной четырехугольной пирамиде сторона основания равна 2 см, высота 1 см. Найдите площадь части сферы с центром в вершине пирамиды и радиусом 1 см, заключенной внутри пирамиды.

17. Чему равна площадь сферического треугольника на единичной сфере, все углы которого равны: а) 80°; б) 90°; в) 100°?

18. Выведите формулу площади сферического n-угольника на сфере радиуса R, все углы которого равны j. В каких пределах может изменяться j?