РАВНОСОСТАВЛЕННОСТЬ И ЗАДАЧИ НА РАЗРЕЗАНИЕ
Две
фигуры называются равносоставленными, если они могут быть разложены на
одинаковое число попарно равных фигур.
Из свойств площади следует,
что равносоставленные фигуры равновелики. В частности, равносоставленные
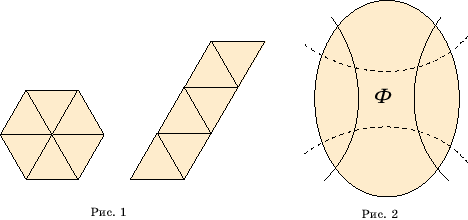
многоугольники равновелики. Например, изображенные на рисунке 1 правильный
шестиугольник и параллелограмм – равносоставленные фигуры, так как оба они
составлены из шести равных равносторонних треугольников.
Естественно поставить обратный вопрос: "Всякие ли два равновеликих
многоугольника равносоставлены?" Утвердительный ответ был получен в XIX
веке.
Теорема. Любые два равновеликих многоугольника равносоставлены.
Доказательство этой теоремы
будет получено как результат применения нескольких теорем.
Теорема 1. Две фигуры, равносоставленые с одной и той же фигурой,
равносоставлены.
Доказательство. Действительно, пусть фигуры Ф' и Ф''
равносоставлены с фигурой Ф. Рассмотрим линии, разбивающие фигуру Ф
на части, из которых можно составить фигуру Ф' и кроме того линии,
разбивающие фигуру Ф на части, из которых можно составить фигуру Ф''
(рис. 2). Те и другие линии разбивают фигуру Ф на более мелкие части, из
которых можно составить как фигуру Ф', так и Ф''. Таким образом,
фигуры Ф' и Ф'' равносоставлены.
Теорема 2. Любые два равновеликих параллелограмма
равносоставлены.
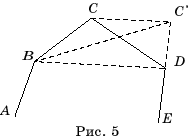
Доказательство. Рассмотрим сначала два параллелограмма с равными
основаниями (рис. 3). По условию они равновелики, значит, имеют равные высоты.
Проведем внутри каждого параллелограмма отрезки, параллельные сторонам другого
параллелограмма. Тогда оба параллелограмма разобьются на одинаковое число
попарно равных фигур, т.е. они равносоставлены.
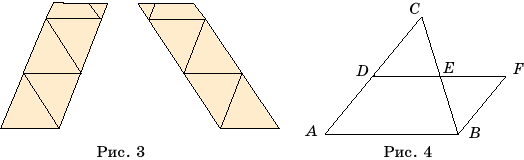
Пусть
теперь параллелограммы не имеют равных сторон. Построим третий параллелограмм,
имеющий с первым одинаковые основание и высоту. Поскольку при этом другую
сторону третьего параллелограмма можно выбирать произвольно, сделаем ее, равной
одной из сторон второго параллелограмма. Тогда третий параллелограмм будет
равновелик и с первым, и со вторым параллелограммами, и с каждым из них имеет
по равной стороне. Следовательно, он равносоставлен и с первым, и со вторым. В
силу теоремы 1 первый и второй параллелограммы равносоставлены.
Теорема 3. Любые два равновеликих треугольника равносоставлены.
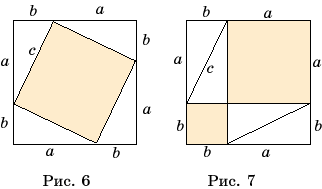
Доказательство. Каждый треугольник продолжением средней линии
преобразуется в равновеликий ему параллелограмм (рис. 4). Поэтому два
равновеликих треугольника преобразуются в два равновеликих
параллелограмма. В силу теоремы 2 эти параллелограммы равносоставлены и,
следовательно, равносоставлены исходные треугольники.
Теорема 4. Всякий многоугольник равносоставлен с некоторым
треугольником.
Доказательство. Рассмотрим многоугольник ABCDE…, и одну из его вершин например, C перенесем
параллельно диагонали BD на продолжение стороны DE (рис. 5). При
этом исходный многоугольник преобразуется в равновеликий многоугольник с числом
сторон на единицу меньшим. Имея в виду, что мы заменили один треугольник другим
- равновеликим, а остальная часть многоугольника осталась неизменной, получим,
что новый многоугольник будет равносоставлен с исходным. Продолжая этот
процесс, мы превратим исходный многоугольник в равносоставленный с ним треугольник.
Приступим
теперь к доказательству основной теоремы. Пусть М' и М'' -
равновеликие многоугольники. Рассмотрим равносоставленные с ними треугольники Т'
и Т'' соответственно. Эти треугольники равновелики и, следовательно,
равносоставлены. Значит, равносоставлены и исходные многоугольники М' и М''.
Доказанная теорема позволяет
в принципе разрезать один из двух равновеликих многоугольников на части и
складывать из них другой многоугольник. Однако это приводит к большому числу
мелких многоугольников. В конкретных примерах, как правило, можно указать
гораздо более рациональный способ разрезания.
В качестве применения метода
разрезания рассмотрим доказательство теоремы Пифагора. С точки зрения площадей,
ее можно переформулировать в следующем виде.
Теорема. Площадь квадрата, построенного на гипотенузе
прямоугольного треугольника, равна сумме площадей квадратов, построенных на
катетах.
Доказательство. Пусть дан прямоугольный треугольник ABC с
катетами a, b и гипотенузой c. Доказательство следует из
рассмотрения двух равных квадратов со стороной, равной сумме катетов данного
прямоугольного треугольника, в которых проведены отрезки, как показано на
рисунках 6, 7. В первом случае квадрат разобьется на квадрат, построенный на
гипотенузе данного треугольника и четыре треугольника, равных данному. Во
втором случае квадрат разобьется на два квадрата, построенных на катетах
данного треугольника и четыре треугольника, равных данному. Таким образом, c2
= a2 + b2.
Задачи
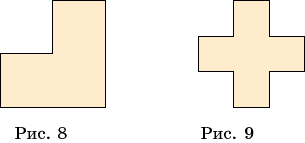
1. Разрежьте фигуру,
изображенную на рисунке 8, на четыре равные части.
1. Греческий крест (рис. 9)
разрежьте на несколько частей и составьте из них квадрат.
3. Греческий крест разрежьте двумя разрезами и из образовавшихся частей сложите квадрат.
4. Даны два квадрата.
Разрежьте один квадрат на четыре части, и из этих частей и другого квадрата
сложите квадрат.
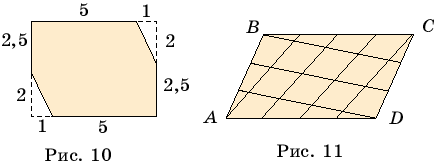
5. Шестиугольник,
изображенный на рисунке 10, разрежьте на две части, из которых можно сложить
квадрат.
6. Используя разрезания
докажите, что площадь правильного восьмиугольника равна произведению его
наибольшей и наименьшей диагоналей.
7. Стороны АВ и CD
параллелограмма ABCD площади 1 разбиты на n равных частей, AD
и ВС - на m равных частей. Точки деления соединены так, как
показано на рисунке 11, где n = 3, m = 4. Чему равны площади
образовавшихся при этом маленьких параллелограммов?
8. Докажите, что никакой выпуклый 13-угольник нельзя разрезать на параллелограммы.
Литература
1. Барр Ст. Россыпи
головоломок. – М.: Мир, 1987.
2. Гарднер М. Есть идея! –
М.: Мир, 1982.
3. Прасолов В.В. Задачи по
планиметрии. – 2-е изд. – Часть II. – М.: Наука, 1991.
4. Линдгрен Г. Занимательные
задачи на разрезание. – М.: Мир, 1977.
5. Савин А.П. Задачи на
разрезание //Квант. – 1987. - № 7.
6. //Квант. – 1988. - № 8.
7. Смирнова И.М. В мире
многогранников. – М.: Просвещение, 1995, с.108, с. 113.