ЗОЛОТОЕ СЕЧЕНИЕ

С давних времен люди занимались поисками гармонии и совершенства. Древние греки считали, что мир устроен по законам гармонии и задача познания мира, таким образом, является задачей поиска гармонии.

Одним из вопросов, волновавших древних ученых, был вопрос о на­хождении наилучшего соотношения неравных частей, составляющих вместе единое целое. Его решение связывают с именем Пифагора, который устано­вил, что наиболее совершенным делением целого на две неравные части является такое деление, при котором меньшая часть так относится к большей, как большая часть относится ко всему целому. В Древней Греции такое деление называлось гармоническим отношением. Интерес к нему нео­бычайно возрос в эпоху Возрождения (XV - XVII). В 1509 году итальянс­кий математик, монах Лука Пачоли (1445 – ок.1514), друг Леонардо да Винчи (1452 – 1519), написал це­лую книгу "О божественной пропорции". Леонардо выполнил иллюстрации к этой книге. В ней воздействие божественной пропорции на человека назы­валось "существенным, невыразимым, чудесным, неизъяснимым, неугасимым, возвышенным, превосходнейшим, непостижимым". Пачоли назвал гармоничес­кое отношение божественной пропорцией ("Sectio Divina"). Термин золо­тое сечение ("Sectio aurea") появился в Германии в первой половине XIX века.

Выясним, каким числом выражается золотое сечение. Для этого выберем произвольный отрезок и примем его длину за единицу. Ра­зобьем этот отрезок на две неравные части. Большую обозначим через x. Тогда меньшая часть равна 1-x. По определению золотого се­чения должно выполняться равенство  Мы получили уравне­ние относительно x, которое легко свести к квадратному x²+x-1 = 0. По­ложительный корень этого уравнения выражается формулой

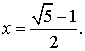
Полученное число обозначается буквой . Это первая буква в имени великого древнегреческого скульптора Фидия, который часто использовал золотое сечение в своих произведениях. Самыми знаменитыми из них были статуи Зевса Олимпийского (которая считалась одним из семи чудес све­та) и Афины Парфенос.

Для нахождения приближений числа  можно воспользоваться числами Фибоначчи. Напомним, что числами Фибоначчи называются числа, задаваемые последовательностью 1, 1, 2, 3, 5, 8, 13, …, в которой два первых числа равны 1, и каждое следующее число равно сумме двух предыдущих, т.е. a_n+1 = a_n + a_n-1. Разделим последнее равенство, почленно, на a_n. Получим равенство 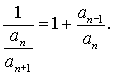 Из него следует, что отношение предыдущего числа к последующему будет стремиться к числу, удовлетворяющему уравнению  т.е. к .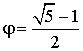

Таким образом, в качестве приближений к числу  можно взять числа последовательности 1, 1/2, 2/3, 3/5, 5/8, 8/13, … .

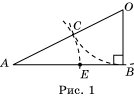
Разделим данный отрезок AB в золотом отношении с помощью циркуля и линейки. Для этого через точку B проведем прямую, перпендикулярную AB, и отложим на ней отрезок BO=AB (рис. 1), затем на OA отложим OC=OB и на AB отложим AE=AC, точка E будет делить отрезок AB в золотом отношении.

Число 1:=1+= 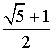обозначим буквой . Из соотношения

следует, что число  можно представить в виде бесконечной дроби

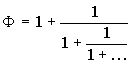
Из соотношения  следует, что число  можно представить в виде

.

Еще раз подчеркнем, что пропорции золотого сечения создают впе­чатление гармонии, красоты. Поэтому скульпторы, архитекторы, художники использовали и используют золотое сечение в своих произведениях. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Причем не только вся статуя, но и от­дельные ее части делятся в золотом отношении.

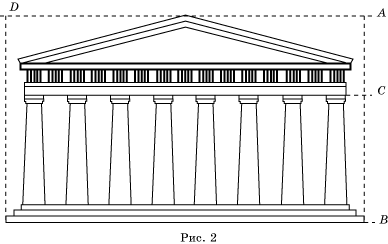
Одно из красивейших произведений древнегреческой архитектуры - Парфенон в Афинах (V в. до н.э.) содержит в себе золотые пропорции. Так, отношение высоты AB здания к его длине AD равно . Если произвести деление высоты Парфенона по золотому сечению, то получим те или иные выступы здания (рис. 2).

Известный русский архитектор М.Ф. Казаков тоже широко использовал в своем творчестве золотое сечение. Его можно обнаружить, например, в архитектуре здания бывшего Сената в Кремле. По проекту М.Ф. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей им. Н.И. Пирогова (Ленинский просп., д. 8).

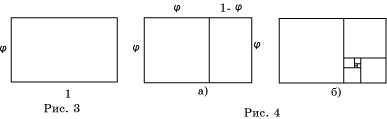
Прямоугольник, стороны которого находятся в золотом отношении, называют золотым прямоугольником (рис. 3). Золотые прямоугольники обладают мно­гими интересными свойствами.

Из определения золотых прямоугольников непосредственно следует, что все они подобны.

Если от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямо­угольник меньших размеров (рис. 4, а). Это непосредственно следует из равенства 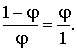Если этот процесс продолжить, то мы получим так называемые вращающи­еся квадраты, и весь прямоугольник окажется составленным из этих квадратов (рис. 4, б).

Если вершины квадратов соединить плавной кривой, то получим кривую, называемую золотой спиралью (рис. 5).

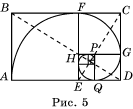
Докажем, что пересечением золотых прямоугольников на рисунке 5 является точка пересечения диагоналей BD и CE. Действительно, из подобия золотых прямоугольников ABCD и EHGD следует, что диагональ HD лежит на диагонали BD. Аналогично, диагональ PE золотого прямоугольника EHPQ лежит на диагонали CE золотого прямоугольника EFCD. Значит, точка пересечения диагоналей прямоугольников первого и второго прямоугольников совпадает с точкой пересечения диагоналей третьего и четвертого прямоугольника. Повторяя эти рассуждения для следующих золотых прямоугольников, получим, что точка пересечения диагоналей принадлежит всем прямоугольникам и, следовательно, является точкой их пересечения.

Помимо золотых прямоугольников имеются и золотые треугольники. Равнобедренный треугольник называется золотым, если его боковая сторона и основание находятся в золотом отношении.

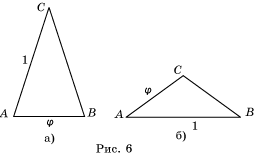
Возможны два типа золотых треугольников (рис. 6, а, б).  В первом случае AB/AC =. Во втором случае AC/AB =.

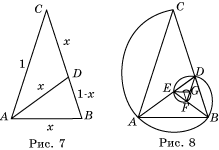
Покажем, что угол при вершине золотого треугольника в первом равен 36, во втором – 118. Для этого в равнобедренном треугольнике ABC с углом при вершине C равным 36 проведем отрезок AD так, что CAD = 36 (рис. 7). Тогда треугольники ACD и ABD равнобедренные и треугольник BDA подобен треугольнику ABC. Примем боковую сторону треугольника ABC за единицу, а его основание за x. Тогда AD = CD = x, BD = 1-x. Из подобия треугольников получаем равенство

из которого следует, что x =, т.е. треугольник ABC – золотой. Кроме того, треугольник ACD, с углом при вершине D равным 118, также – золотой.

          Из выражения для углов золотых треугольников непосредственно следует, что sin 18 = 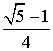, sin 54= .

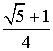В золотом треугольнике ABC, аналогично тому, как это делалось для золотого прямоугольника, можно построить последовательность вращающихся золотых треугольников (рис. 8). Соединяя вершины этих треугольников плавной кривой, получим золотую спираль.

Золотую спираль можно заметить в созданиях природы. Например, раковины многих моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из наиболее распространенных пауков, эпейра, сплетает свою паутину по золотой спирали. Природа повторяет свои находки как в малом, так и в большом, например, семечки в подсолнухе располагаются по золотой спи­рали точно также, как закручиваются многие галактики, в частности и галактика Солнечной системы.

Можно сказать, что золотое сечение, золотой прямоугольник, золотые треугольники, и золо­тая спираль являются математическими символами идеального соотношения формы и роста. Великий немецкий поэт Иоган Вольфган Гете считал их да­же математическими символами жизни и духовного развития.

 

Упражнения

1. Принимая точку A за начало координат, AD – за ось Ox, AB – за ось Oy, найдите координаты точки пересечения золотых прямоугольников (рис. 5).

2. Докажите, что DF параллельно AC, EG параллельно AB (рис. 8).

3. Докажите, что точкой пересечения вращающихся золотых треугольников является точка пересечения отрезков CF  и AG (рис. 8).

4. На рисунке (рис. 9) изображен лотарингский крест, служивший эмблемой «Свободной Франции» (организации, которую в годы второй мировой войны возглавлял генерал де Голль). Он составлен из 13 единичных квадратов. Докажите, что прямая, проходящая через точку A и делящая лотарингский крест на две равновеликие части, делит отрезок BC в золотом отношении.

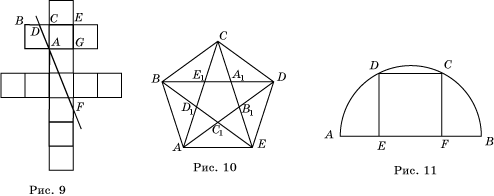
5. На рисунке 10 изображен правильный пятиугольник с проведенными в нем диагоналями, образующими звездчатый правильный пятиугольник – пентаграмму. Легко видеть, что все треугольники, на которые при этом разбивается пятиугольник, являются золотыми.

6. Сторона правильного пятиугольника равна 1. Найдите его диагональ.

7. Докажите, что диагонали правильного пятиугольника образуют правильный пятиугольник. Найдите сторону этого пятиугольника, если сторона исходного пятиугольника равна 1.

8. Найдите радиус окружности, описанной около правильного десятиугольника со стороной 1.

9. В полукруг с диаметром АВ вписан квадрат CDEF (рис. 11). До­кажите, что отрезок АЕ и сторона квадрата ED находятся в золотом отно­шении.

10. Найдите: а) cos 18; б) cos 54.

11. На рисунке 12 изображен малый звездчатый додекаэдр. Его можно получить, надставив на гранях додекаэдра правильные пятиугольные пирамиды. Какими при этом должны быть боковые ребра этих пирамид, чтобы грани, закрашенные одним цветом, лежали в одной плоскости, если ребро додекаэдра равно 1?

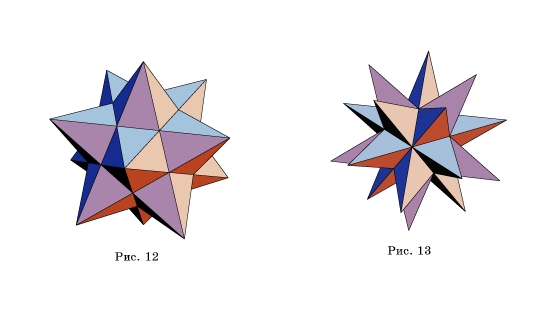
12. На рисунке 13 изображен большой звездчатый додекаэдр. Его можно получить, надставив на гранях икосаэдра правильные треугольные пирамиды. Какими при этом должны быть боковые ребра этих пирамид, чтобы грани, закрашенные одним цветом, лежали в одной плоскости, если ребро икосаэдра равно 1?

13. На рисунке 14 изображен большой додекаэдр. Его можно получить, вырезав из граней икосаэдра правильные треугольные пирамиды. Какими при этом должны быть боковые ребра этих пирамид, чтобы грани, закрашенные одним цветом, лежали в одной плоскости, если ребро икосаэдра равно 1?

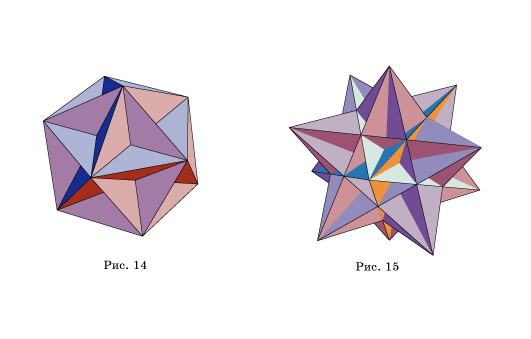
14. На рисунке 15 изображен большой икосаэдр. Его можно получить, вырезав из граней малого звездчатого додекаэдра треугольные пирамиды. Какими при этом должны быть боковые ребра и углы этих пирамид, чтобы грани, закрашенные одним цветом, лежали в одной плоскости, если ребро додекаэдра равно 1?

 

Литература

1. Азевич А.И. От золотой пропорции к ее "производным". // Квант – 1995. - № 3. – С. 55.

2. Бендукидзе А.Д. Золотое сечение. // Квант. – 1973. - № 8. – С. 22.

3. Васютинский Н.А. Золотая пропорция. – М.: Молодая гвардия, 1990.

4. Виленкин Н.Я. и др. За страницами учебника математики, 10-11. – М.: Просвещение, 1996.

5. Волошинов А.В. Математика и искусство. – М.: Просвещение, 1992.

6. Воробьев Н.Н. Числа Фибоначчи. – 6-ое изд., доп. – М.: Наука, 1992.

7. Гарднер М. Число  - золотое сечение / В кн. Математические головоломки и развлечения. – М.: Мир, 1971.

8. Еще раз о золотом сечении. // Квант. – 1989. - № 8. – С. 75.

9. Жуков А., Савин А. Числа Фидия и золотое сечение // Энциклопедия для детей. – т. 11. – М.: Аванта, 1998.

10. Избранные вопросы математики. 10 класс. – М.: Просвещение, 1980.

11. Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1966.

12. Левитин К. Геометрическая рапсодия. – 2-ое изд. – М.: Знание. – 1984.

13. Пидоу Д. Геометрия и искусство. – М.: Мир. – 1979.

14. Прохоров А.И. Золотая спираль // Квант. – 1984. - № 9. – С. 15.

15. Смирнова И.М. В мире многогранников. – М.: Просвещение. – 1995.

16. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов. – М.: Мнемозина, 2005.

17. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. – М.: Стройиздат. – 1990.