ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ
Тетраэдр
является одним из простейших многогранников, гранями которого являются четыре
треугольника. Его можно считать пространственным аналогом треугольника.
Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке –
центре вписанной окружности.
Теорема 1'. Биссектральные плоскости двугранных углов тетраэдра
пересекаются в одной точке – центре вписанной сферы.
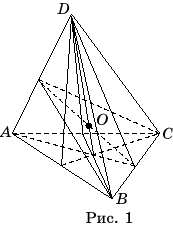
Доказательство. Пусть ABCD – тетраэдр. Пересечением
биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC
(рис. 1) является точка O, равноудаленная от всех граней тетраэдра.
Следовательно, эта точка принадлежит биссектральным плоскостям остальных
двугранных углов тетраэдра и является центром вписанной сферы.
Теорема
2. Серединные перпендикуляры к
сторонам треугольника пересекаются в одной точке – центре описанной окружности.
Теорема 2'. Плоскости, проходящие через середины ребер тетраэдра
и перпендикулярные этим ребрам, пересекаются в одной точке – центре описанной
сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением
плоскостей, проходящих через середины ребер AD, BD, и CD
является точка O, равноудаленная от всех вершин тетраэдра.
Следовательно, эта точка принадлежит остальным плоскостям и является центром
описанной сферы.
Теорема 2". Прямые, перпендикулярные граням тетраэдра, и
проходящие через центры их описанных окружностей, пересекаются в одной точке –
центре описанной сферы.
Доказательство. Каждая такая прямая является геометрическим местом
точек, равноудаленных от вершин соответствующей грани тетраэдра. Поэтому центр
описанной сферы будет принадлежать всем этим прямым.
Заметим, что не у всякого
тетраэдра прямые, проходящие через центры вписанных в грани окружностей и
перпендикулярные этим граням, пересекаются в одной точке. Ответ на то, когда
это происходит, дает следующая теорема.
Теорема 2'''. У тетраэдра существует сфера, касающаяся всех его
ребер, тогда и только тогда, когда суммы противоположных ребер этого тетраэдра
равны.
Доказательство. Пусть у тетраэдра ABCD существует сфера,
касающаяся его ребер. Обозначим через a, b, c и d расстояния от
соответствующих вершин тетраэдра до точек касания. Тогда AB = a + b, CD = c
+ d. Следовательно, AB + CD = a + b + c + d. Аналогично, AC + BD
= a + b + c + d, AD + BC = a + b + c + d. Таким образом, суммы
противоположных ребер тетраэдра равны.
Обратно. Предположим, что
суммы противоположных ребер тетраэдра ABCD равны. Впишем в треугольник ABC
окружность. Обозначим через X точку касания этой окружности стороны AB
(рис. 2).
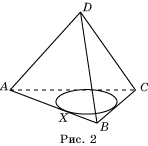
Тогда AX = (AB + AC – BC):2. Так как AC – BC = AD – BD, то AX = (AB + AD – BD):2.
Следовательно, точка X является
точкой касания окружности, вписанной в треугольник ABD. Через центры этих двух окружностей проведем
перпендикуляры. Они лежат в одной плоскости, проходящей через X и
перпендикулярной AB. Точка O их пересечения будет равноудалена от
сторон треугольников ABC и ABD. Таким образом, любые два
перпендикуляра, проходящие через центры окружностей, вписанных в грани
тетраэдра, пересекаются. Из этого следует, что или они лежат в одной плоскости,
или пересекаются в одной точке. Поскольку они не лежат в одной плоскости, то
значит, они пересекаются в одной точке O, равноудаленной от всех ребер тетраэдра, т.е. O
– центр сферы, касающейся всех ребер данного тетраэдра.
Теорема 3. Медианы треугольника пересекаются в одной точке,
называемой центроидом треугольника и делятся в этой точке в отношениии 2 : 1.
Теорема 3'. Отрезки, соединяющие вершины тетраэдра с точками
пересечения медиан противоположных граней, пересекаются в одной точке –
центроиде тетраэдра и делятся в этой точке в отношении 3 : 1, считая от
вершины.
Доказательство. Пусть ABCD –
тетраэдр, O – точка пересечения медиан треугольника ABC, P –
точка пересечения медиан треугольника BCD, R – точка пересечения
отрезков DO и AP (рис.
3).
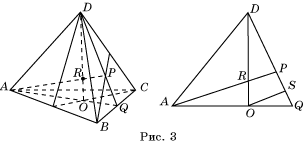
Рассмотрим треугольник AQD.
Точки O и P делят соответствующие стороны в отношении 2 : 1.
Покажем, что точка R делит DO и AP в отношении 3 : 1. В
треугольнике APQ проведем OS параллельно AP. Она разделит
отрезок PQ в отношении 2 : 1. Если отрезок SQ принять за единицу,
то отрезок DP будет равен 6. Отрезки DR и RQ относятся
также как DP и PS, т.е. DR : RQ = 6 : 2 = 3 : 1.
Аналогичным образом доказывается, что точка R делит отрезок AP в
отношении 3 : 1. Отрезки, соединяющие вершины B и C с точками
пересечения медиан противоположных граней также будут делить отрезок DO
в отношении 3 : 1 и, следовательно, будут проходить через точку O.
Что и требовалось доказать.
Теорема 4. Отрезки, соединяющие середины противоположных ребер
тетраэдр, пересекаются в одной точке – центроиде.
Доказательство. Достаточно заметить, что в предыдущем доказательстве
медиана треугольника AQD, проведенная из вершины Q, проходит
через центроид O.
Теорема 5. Для цетроида O треугольника ABC имеет
место равенство ![]() .
.
Теорема 5'. Для цетроида O тетраэдра ABCD имеет
место равенство ![]() .
.
Теорема 6. Пусть a произвольная прямая, проходящая через
центроид треугольника ABC. Будем считать одну из полуплоскостей, на
которые эта прямая разбивает плоскость, положительной, а другую отрицательной.
Тогда сумма расстояний от вершин треугольника до прямой a, взятых со
знаком + или – в зависимости от того, какой полуплоскости принадлежит вершина,
равна нулю.
Теорема 6'. Пусть ![]() произвольная
плоскость, проходящая через центроид тетраэдра ABCD. Будем считать одно
из полупространств, на которые эта плоскость разбивает пространство,
положительным, а другое отрицательным. Тогда сумма расстояний от вершин
тетраэдра до плоскости
произвольная
плоскость, проходящая через центроид тетраэдра ABCD. Будем считать одно
из полупространств, на которые эта плоскость разбивает пространство,
положительным, а другое отрицательным. Тогда сумма расстояний от вершин
тетраэдра до плоскости ![]() , взятых со знаком + или – в зависимости от того, какому
полупространству принадлежит вершина, равна нулю.
, взятых со знаком + или – в зависимости от того, какому
полупространству принадлежит вершина, равна нулю.
Теорема 7. Пусть a произвольная прямая. Будем считать одну
из полуплоскостей, на которые эта прямая разбивает плоскость, положительной, а
другую отрицательной. Тогда сумма расстояний от вершин треугольника до прямой a,
взятых со знаком + или – в зависимости от того, какой полуплоскости принадлежит
вершина, равна утроенному расстоянию от центроида треугольника до прямой a.
Теорема 7'. Пусть a произвольная плоскость. Будем
считать одно из полупространств, на которые эта плоскость разбивает пространство,
положительным, а другое отрицательным. Тогда сумма расстояний от вершин
тетраэдра до плоскости a , взятых со знаком + или – в зависимости от того,
какому полупространству принадлежит вершина, равна учетверенному расстоянию от
центроида тетраэдра до данной плоскости.
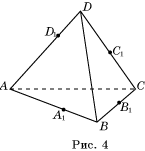
Теорема 8' (Менелая). Пусть на ребрах AB, BC, CD и
AD тетраэдра ABCD взяты соответственно точки A1, B1, C1 и D1. Для того чтобы эти точки лежали в одной плоскости,
необходимо и достаточно, чтобы выполнялось равенство
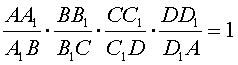 .
.
Доказательство. Пусть точки A1, B1, C1
и D1 лежат в одной плоскости (рис. 4). Опустим из вершин
тетраэдра перпендикуляры AA’, BB’, CC’, DD’ на эту
плоскость. Тогда AA1:A1B = AA’:BB’, BB1:B1C = BB’:CC’, CC1:C1D = CC’:DD’, DD1:D1A = DD’:AA’. Откуда и
следует требуемое равенство.
Обратно,
пусть выполняется указанное равенство. Через точки A1, B1, C1 проведем
плоскость. Она пересечет ребро AD в некоторой точке D’. Для точек A1, B1, C1 и D’ также
выполняется указанное равенство. Из этого следует, что DD1:D1A = DD’:D’A и, значит,
D1 и D’ совпадают, т.е. A1, B1, C1 и D1 лежат в
одной плоскости.
Теорема 9' (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A1, B1, C1 и D1. Плоскости ABC1, BCD1, CDA1 и DAB1 пересекаются в одной точке тогда и только тогда, когда
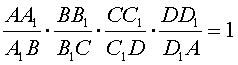 .
.
Доказательство. По предыдущей теореме выполнимость указанного
равенства равносильна тому, что точки A1, B1, C1 и D1
лежат в одной плоскости. При этом точка пересечения
этих плоскостей является точкой пересечения диагоналей четырехугольника A1B1C1D1.
Рассмотрим
теперь некоторые специальные тетраэдры.
Равногранным тетраэдром
называется тетраэдр, у которого все грани равны.
Теорема 10. Для любого остроугольного треугольника существует
равногранный тетраэдр, грани которого равны данному треугольнику.
Доказательство. Пусть ABC
– произвольный остроугольный треугольник.
Через его вершины проведем прямые, параллельные противоположным сторонам (рис.
5).
Они
образуют треугольник A1B1C1,
разбитый на четыре треугольника, равных исходному. Ясно, что A1B1C1 представляет
собой развертку равногранного тетраэдра.
Теорема 11. Тетраэдр является равногранным тогда и только тогда,
когда у него центры вписанной и описанной сфер совпадают.
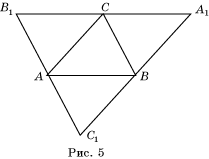
Доказательство. Пусть в тетраэдре ABCD центрами вписанной и
описанной сфер является точка O. P и Q – и точки
касания вписанной сферы граней ABC и BCD (рис.6). Заметим, что P и
Q являются центрами окружностей, описанных около
треугольников ABC и BCD соответственно. Из этого, в
частности, следует, что треугольник ABC –
остроугольный. Кроме того, треугольники BPC и BQC равны. Углы BAC и BDC равны половинам
углов BPC и BQC, и следовательно также равны. Таким образом, плоские
углы при вершине D равны углам треугольника ABC. Значит, в сумме
они составляют 1800.
Аналогично, плоские углы при остальных вершинах тетраэдра в сумме составляют
1800. Поэтому развертка этого
тетраэдра имеет вид, указанный в теореме 1. Следовательно, тетраэдр
равногранный.
Покажем
обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной
сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового
радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны
и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все
плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра,
проведенной из вершины с прямыми плоскими углами, является точка пересечения
высот противоположной грани.
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного
тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме
квадратов площадей остальных граней этого тетраэдра.
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при
вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D
через a, b, c, а затем воспользоваться формулой Герона для нахождения
площади треугольника ABC.
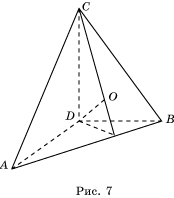
Мы
рассмотрим другой способ. Имеем SADB = SABC cos![]() ; SACD = SABC cos
; SACD = SABC cos ![]() ; SBCD = SABCcos
; SBCD = SABCcos ![]() , где
, где ![]() ,
, ![]() ,
, ![]() - соответствующие двугранные углы, равные углам CDO, BDO и ADO. Таким
образом, cos
- соответствующие двугранные углы, равные углам CDO, BDO и ADO. Таким
образом, cos ![]() , cos
, cos ![]() , cos
, cos ![]() составляют координаты
единичного вектора, поэтому cos2
составляют координаты
единичного вектора, поэтому cos2![]() + cos2
+ cos2![]() + cos2
+ cos2![]() = 1. Значит, S2ABC = S2ABD + S2BCD + S2ACD. Что и требовалось доказать.
= 1. Значит, S2ABC = S2ABD + S2BCD + S2ACD. Что и требовалось доказать.
Ортогональным называется тетраэдр, у которого противоположные ребра
попарно перпендикулярны.
Ортоцентрическим называется тетраэдр, у которого высоты или их
продолжения пересекаются в одной точке – ортоцентре третаэдра.
Теорема 14. Тетраэдр является ортогональным тогда и только тогда,
когда отрезки, соединяющие середины противоположных ребер, равны.
Доказательство. Пусть ABCD – тетраэдр. A1, B1, C1, D1– середины двух
пар противоположных ребер (рис. 8).
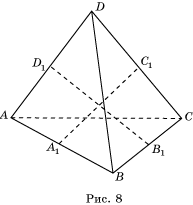
Тогда
A1B1D1C1– параллелограмм.
Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC ![]() BD.
BD.
Теорема 2. Тетраэдр является ортогональным тогда и только тогда,
когда он является ортоцентрическим.
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD2– высота, опущенная из вершины D. Плоскость CDD2
перпендикулярна
AB и, следовательно, DC1 и CC1– высоты треугольников ABC и ABD. Высоты DD2
и CC2 треугольника C1CD
пересекаются.
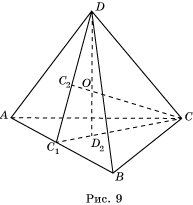
Таким
образом, произвольные пары высот тетраэдра пересекаются в одной точке. Но
попарно пересекающиеся прямые или лежат в одной плоскости, или пересекаются в
одной точке. В нашем случае прямые не лежат в одной плоскости и, следовательно,
пересекаются в одной точке O.
Обратно, пусть высоты
тетраэдра ABCD пересекаются в одной точке O. Тогда DD2![]() ABC
и, следовательно, DD2
ABC
и, следовательно, DD2![]() ABC. Аналогично, CC2
ABC. Аналогично, CC2![]() ABD
и, следовательно, CC2
ABD
и, следовательно, CC2![]() AB. Таким образом, AB перпендикулярна плоскости COD
и, следовательно, AB
AB. Таким образом, AB перпендикулярна плоскости COD
и, следовательно, AB ![]() CD. Аналогично показывается перпендикулярность остальных
противоположных ребер.
CD. Аналогично показывается перпендикулярность остальных
противоположных ребер.
Теорема 3. Тетраэдр является ортогональным тогда и только тогда,
когда одна из его высот проходит через ортоцентр соответствующей грани.
Доказательство. Необходимость вытекает из Теоремы 2. Покажем
достаточность. Пусть D2 –
ортоцентр грани ABC, DD2 – высота тетраэдра ABCD. Тогда BC перпендикулярна
плоскости AA1D и, следовательно, BC перпендикулярна AD.
Аналогично показывается перпендикулярность остальных противоположных ребер.
Теорема 4. В ортогональном тетраэдре окружности 9-ти точек всех
граней лежат на одной сфере (сфера 24 точек).
Доказательство. Рассмотрим сферу с центром в центроиде тетраэдра и
диаметром, равным отрезкам, соединяющим середины противоположных ребер. Эта
сфера проходит через середины всех ребер тетраэдра и, следовательно, содержит
окружности 9 точек всех граней.
Литература
1. Адамар Ж. Элементарная геометрия. Часть II.
Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии.
Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по
стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом.
Избранные задачи и теоремы элементарной математики. Часть 3. – М.:
Государственное издательство технико-теоретической литературы, 1954.