И.М. СМИРНОВА, В.А. СМИРНОВ
П А Р
К Е Т Ы
2009
Паркеты с древних времен привлекали к себе
внимание людей. Ими мостили дороги, украшали полы в помещениях, стены домов,
использовали в декоративно-прикладном искусстве. Знаменитый голландский художник
Мариус Эшер (1898-1972) посвятил паркетам несколько своих картин. Среди них:
"Всадники" (рис. 1), "Ящерицы" (рис. 2), "Летящие
птицы" (рис. 3).


Проявление свойств паркетов сказывается на
свойствах различных природных минералов и кристаллов. В то же время паркеты
являются объектом исследования математиков. Глубокие результаты здесь получены
отечественными учеными, академиками: А.Д. Александровым, Б.Н. Делоне, Е.С.
Федоровым и др.
Здесь мы рассмотрим паркеты на евклидовой
плоскости, на плоскости Лобачевского, на сфере и в пространстве.
1.
Паркеты на плоскости
Паркетом на плоскости
называется такое заполнение плоскости многоугольниками, при котором любые два
многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не
имеют общих точек.
Паркет называется правильным, если он
состоит из равных правильных многоугольников.
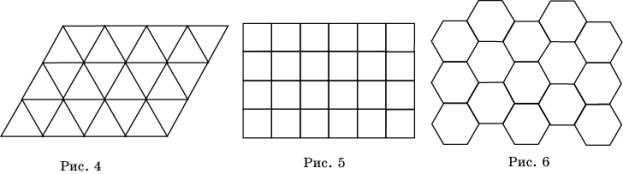
Примеры правильных паркетов дают заполнения
плоскости:
а)
правильными треугольниками (рис. 4);
б)
квадратами (рис. 5);
в)
правильными шестиугольниками (рис. 6).
Докажем, что другими равными правильными
многоугольниками заполнить плоскость нельзя. Действительно, углы правильного n-угольника
равны ![]() . Заполним таблицу, состоящую из углов
. Заполним таблицу, состоящую из углов ![]() правильных n-угольников.
правильных n-угольников.
|
N |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
60 |
90 |
108 |
120 |
1284/7 |
135 |
140 |
144 |
1473/11 |
150 |
Если в одной вершине паркета сходится m правильных
n -
угольников, то должно выполняться равенство ![]() откуда
откуда
![]()
Возможными допустимыми значениями n
являются 3, 4 и 6. При остальных
значениях n число m оказывается дробным. В частности,
нельзя заполнить плоскость правильными пятиугольниками.
Можно подумать, что наличие только трех видов
правильных паркетов обусловлено исключительно значениями углов правильных
многоугольников, и если отказаться от требования правильности многоугольников,
то число паркетов увеличится.
На самом деле, это не так. Даже, если отказаться
от выпуклости многоугольников, или допускать в качестве сторон многоугольников
кривые линии, т.е. рассматривать криволинейные многоугольники, то при некоторых
естественных ограничениях на размеры многоугольников (о которых речь пойдет ниже)
имеется только три вида таких паркетов:
1) из треугольников, в каждой вершине которого
сходится шесть сторон;
2) из четырехугольников, в каждой вершине
которого сходится четыре стороны;
3) из шестиугольников, в каждой вершине которого
сходится три стороны.
Мы не будем доказывать это утверждение в общем
виде, а рассмотрим несколько примеров, показывающих причину его справедливости.
Например, выясним, можно ли составить паркет из
треугольников, в каждой вершине которого сходится три стороны.
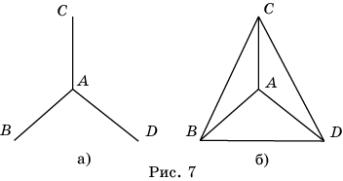
Пусть в вершине A сходится три стороны AB, AC и AD (рис.
7, а). Так как паркет состоит из треугольников, то вершины B, C и D
попарно должны соединяться линиями (рис. 7, б). Но в этом случае в вершинах B, C и D будет
сходиться по три стороны и ни одной стороны нельзя будет добавить для
продолжения паркета. Таким образом, фигуру на рисунке 7, б нельзя достроить до
паркета на всей плоскости, т.е. искомого паркета не существует.
Самостоятельно покажите, что не существует
паркета из треугольников, в каждой вершине которого сходится: а) четыре
стороны; б) пять сторон.
Покажем, что не существует паркета, состоящего из
четырехугольников, в каждой вершине которого сходится три стороны.
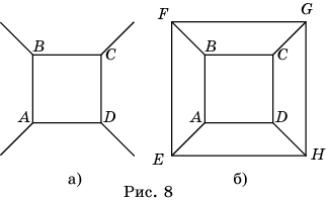
Рассмотрим четырехугольник ABCD (рис.
8, а). Из каждой его вершины должно выходить дополнительно по одной стороне AE, BF, CG, DH. Так
как паркет состоит из четырехугольников, то концы этих сторон E, F, G, H
должны попарно соединяться линиями (рис. 8, б). Но в этом случае в вершинах E, F, G и H будет
сходиться по три стороны и ни одной стороны нельзя будет добавить для
продолжения паркета. Таким образом, фигуру на рисунке 8, б нельзя достроить до
паркета на всей плоскости, т.е. искомого паркета не существует.
Используя рисунок 9, самостоятельно покажите, что
не существует паркета из пятиугольников, в каждой вершине которого сходится три
стороны.
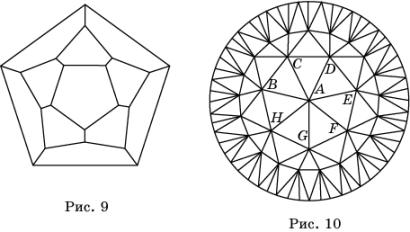
Выясним, существует ли паркет из треугольников, в
каждой вершине которого сходится семь сторон.
Попробуем построить такой паркет. Начнем с
вершины A, в которой
сходится семь сторон. Расположим их концы B, C, D, E, F, G, H на
окружности и соединим их хордами (рис. 10). В результате получим семь
треугольников с общей вершиной A. Из вершин этих треугольников, отличных от A,
должно дополнительно выходить по четыре стороны. Расположим концы этих сторон
на окружности и соединим их хордами. В результате получим еще 28 треугольников.
Этот процесс можно продолжать. Однако при этом придется или уменьшать стороны
треугольников, являющиеся хордами окружностей, или увеличивать стороны
треугольников, соединяющие вершины на соседних окружностях. Если же мы
ограничим стороны треугольников снизу некоторым числом ![]() >0 и сверху некоторым числом
>0 и сверху некоторым числом ![]() >0, то, начиная с некоторого шага, построение паркета
будет невозможным.
>0, то, начиная с некоторого шага, построение паркета
будет невозможным.
Оказывается, что не только это, но и никакое
другое построение паркета из треугольников, в каждой вершине которого сходится
семь сторон с указанными ограничениями, невозможно.
Аналогичным образом, не существует паркетов из
треугольников, в каждой вершине которых сходится восемь или более сторон.
Из рассмотренных выше правильных паркетов из
треугольников, квадратов и шестиугольников можно получать и другие паркеты.
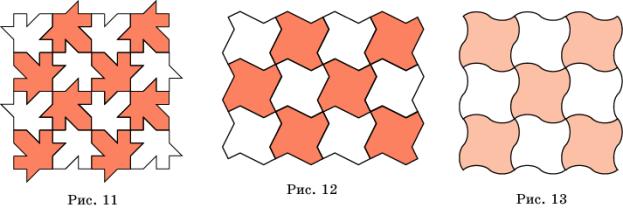
Например, на рисунках 11 – 13 показаны паркеты, полученные из квадратного
паркета.
Самостоятельно получите новые паркеты из треугольного и
шестиугольного паркетов.
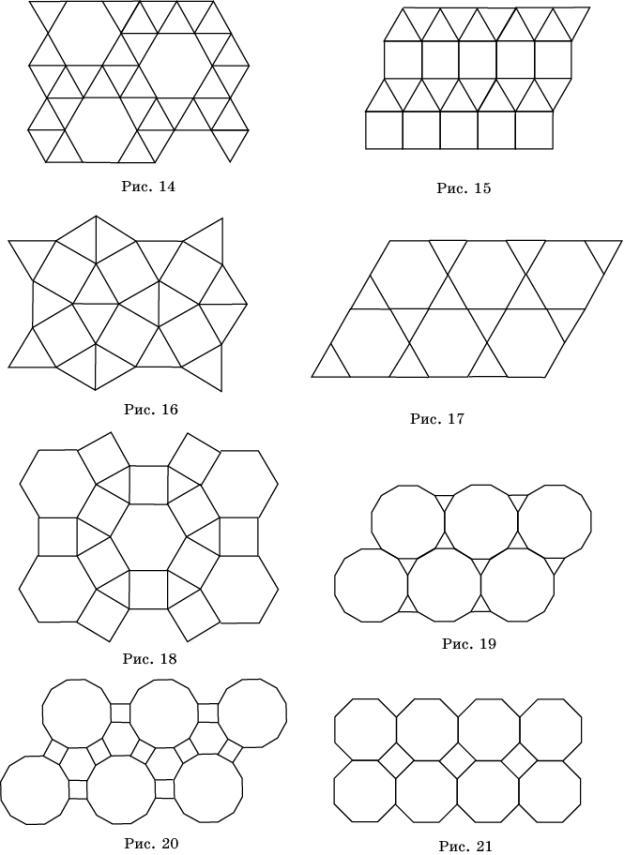
Расширим способы составления паркетов из
правильных многоугольников, разрешив использовать в них правильные
многоугольники с различным числом сторон. Это, так называемые, полуправильные
паркеты.
Паркет называется полуправильным, если он
состоит из правильных многоугольников (возможно с разным числом сторон),
одинаково расположенных вокруг каждой вершины.
Обозначим через ![]() 1,
1, ![]() 2, … углы правильных многоугольников, имеющих
общую вершину. Расположим их в порядке возрастания
2, … углы правильных многоугольников, имеющих
общую вершину. Расположим их в порядке возрастания ![]() 1
1 ![]()
![]() 2
2 ![]() … . Учитывая,
что сумма всех таких углов должна быть равна 360
… . Учитывая,
что сумма всех таких углов должна быть равна 360![]() , составим таблицу, содержащую возможные наборы углов, и
укажем соответствующие паркеты.
, составим таблицу, содержащую возможные наборы углов, и
укажем соответствующие паркеты.
|
|
|
|
|
|
|
|
|
60 |
60 |
60 |
60 |
60 |
60 |
Правильный паркет из 3-ов (рис. 4) |
|
60 |
60 |
60 |
60 |
120 |
|
Паркет из 3-ов и 6-ов (рис. 14) |
|
60 |
60 |
60 |
90 |
90 |
|
Два
паркета из 3-в и 4-в (рис. 15, 16) |
|
60 |
60 |
90 |
150 |
|
|
Нет паркета |
|
60 |
60 |
120 |
120 |
|
|
Паркет из 3-в и 6-в (рис. 17) |
|
60 |
90 |
90 |
120 |
|
|
Паркет из 3-в, 4-в и 6-в (рис. 18) |
|
60 |
150 |
150 |
|
|
|
Паркет из 3-в и 12-в (рис. 19) |
|
90 |
90 |
90 |
90 |
|
|
Правильный паркет из квадратов (рис. 5) |
|
90 |
120 |
150 |
|
|
|
Паркет из 4-в, 6-в и 12-в (рис. 20) |
|
90 |
135 |
135 |
|
|
|
Паркет из 4-в и 8-в (рис. 21) |
|
120 |
120 |
120 |
|
|
|
Правильный паркет из 6-ов (рис. 6) |
Таким образом, всего имеется 8 типов
полуправильных паркетов.
Для числа этих паркетов также существенным
являются не величины углов и сторон, а число сторон в многоугольниках и
вершинах.
Рассмотрим теперь вопрос о заполнении плоскости
неправильными равными многоугольниками.
Теорема. Для
любого четырехугольника существует паркет, состоящий из четырехугольников,
равных исходному. Иначе говоря, четырехугольником произвольной формы можно
заполнить всю плоскость.
Доказательство. Пусть
дан четырехугольник АВСD (рис.
22). Рассмотрим центрально-симметричный ему четырехугольник относительно середины
стороны АВ. Исходный четырехугольник АВСD
обозначим цифрой 1, а симметричный - цифрой 2. Теперь четырехугольник 2 отразим
симметрично относительно середины его стороны ВС. Полученный четырехугольник обозначим цифрой 3 и отразим его
симметрично относительно середины его стороны CD.
Полученный четырехугольник обозначим цифрой 4. Четырехугольники 1, 2, 3 и 4
примыкают к общей вершине углами А, В, С
и D. Поскольку сумма углов четырехугольника равна
360![]() , то эти четырехугольники заполнят часть плоскости вокруг
общей вершины. Такое же построение можно провести вокруг каждой новой вершины,
что и даст искомое заполнение плоскости.
, то эти четырехугольники заполнят часть плоскости вокруг
общей вершины. Такое же построение можно провести вокруг каждой новой вершины,
что и даст искомое заполнение плоскости.
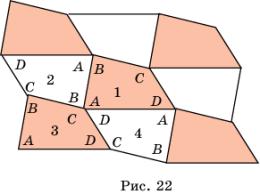
Заметим, что четырехугольники, закрашенные одним
цветом (рис. 22), получаются друг из друга параллельным переносом.
Самостоятельно составьте паркет из равных
невыпуклых четырехугольников.
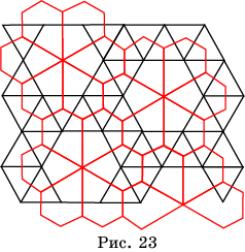
Паркеты из неправильных многоугольников можно
получить из полуправильных паркетов, используя двойственность.
Двойственным к
паркету, состоящему из правильных многоугольников, называется паркет, вершины
которого находятся в центрах многоугольников данного паркета.
Ясно, что двойственным к правильному паркету,
состоящему из треугольников, является правильный паркет, состоящий из
шестиугольников. Двойственным к правильному паркету, состоящему из
шестиугольников, является правильный паркет, состоящий из треугольников.
Правильный паркет, состоящий из квадратов, двойственен сам себе.
На рисунке 23 представлен паркет, состоящий из
пятиугольников, двойственный паркету, изображенному на рисунке 14.
Упражнения
1. Можно ли составить паркет из правильных: а)
пятиугольников; б) шестиугольников; в) семиугольников?
2. Можно ли составить паркет из правильных: а)
восьмиугольников и четырехугольников; б) двенадцатиугольников и треугольников;
в) десятиугольников и пятиугольников?
3. Можно ли составить паркет из равных
треугольников произвольной формы?
4. Можно ли составить паркет из равных четырехугольников
произвольной формы?
5. Нарисуйте паркет, составленный из
четырехугольников, равных четырехугольнику, изображенному на рисунке 24.
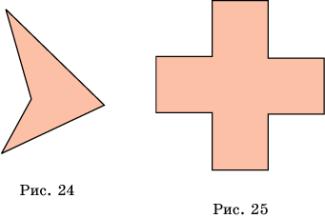
6. Можно
ли составить паркет из равных пятиугольников?
7. Можно ли составить паркет из равных
шестиугольников произвольной формы?
8. Докажите, что с помощью
центрально-симметричных шестиугольников (даже невыпуклых) можно заполнить
плоскость. Приведите пример соответствующего паркета.
9. Попробуйте построить паркет из семиугольников,
в каждой вершине которого сходится три стороны. Возможно ли такое построение
при ограничениях на стороны семиугольников?
10. Составьте паркет из греческих крестов (рис.
25).
11. Нарисуйте паркеты, двойственные к паркетам,
изображенным на рисунках 15-21.
12. Докажите, что паркеты, двойственные к
полуправильным паркетам, состоят из равных многоугольников. Найдите углы этих
многоугольников.
13. Используя паркеты, изображенные на рисунках
14 – 21, нарисуйте паркеты, в каждой вершине которых сходится три стороны, и
состоящие из равных: а) пятиугольников, шестиугольников и двенадцатиугольников;
б) пятиугольников, шестиугольников и восьмиугольников; в) четырехугольников,
шестиугольников, восьмиугольников и двенадцатиугольников; г) треугольников,
восьмиугольников и шестнадцатиугольников.
14. Два равных выпуклых четырехугольника
разрезали: первый - по одной диагонали, а второй - по другой диагонали.
Докажите, что из полученных четырехугольников можно сложить параллелограмм.
15. Выпуклый четырехугольник разрезали на четыре
части по отрезкам, соединяющим середины его противоположных сторон. Докажите,
что из этих частей можно сложить параллелограмм.
16. Придумайте паркеты, составленные из равных
фигур, ограниченных кривыми линиями.
17. Найдите какие-нибудь условия на криволинейный
четырехугольник, при которых из него можно составить паркет.
18. Выясните, как паркет на рисунке 3 может быть
получен искривлением сторон паркета из четырехугольников.
19. Какое наименьшее число красок потребуется для
раскраски правильных паркетов так, чтобы соседние многоугольники были окрашены
в разные цвета?
20. Какое наименьшее число красок потребуется для
раскраски полуправильных паркетов так, чтобы соседние многоугольники были
окрашены в разные цвета?
2. Паркеты на плоскости Лобачевского
Несколько картин Мариуса Эшера
посвящены паркетам на модели Пуанкаре плоскости Лобачевского (рис. 26). Будем
для краткости называть ее плоскостью Лобачевского. Точками
этой плоскости являются точки, расположенные внутри некоторого фиксированного
круга, а прямыми – диаметры без концов и дуги окружностей (рис. 27), лежащих
внутри этого круга и перпендикулярные его окружности. (Углом между двумя
пересекающимися окружностями называется угол между касательными, проведенными в
точке их пересечения.) Для того, чтобы определить равенство фигур на этой
плоскости, напомним определение и свойства инверсии.

Инверсией
относительно данной окружности с центром O и радиусом R называется преобразование, при котором точкам A плоскости,
отличным от O сопоставляются точки A’ на луче OA такие, что OA![]() OA’=R2. Точке O ничего
не сопоставляется. (Иногда точке O сопоставляют бесконечно удаленную точку.)
OA’=R2. Точке O ничего
не сопоставляется. (Иногда точке O сопоставляют бесконечно удаленную точку.)
Ясно, что если точка A
принадлежит окружности, OA = R, то OA’ = R и, следовательно, точка A переходит сама в себя.
Если точка A лежит внутри круга, OA < R, то OA’ > R и, следовательно, точка A переходит в точку вне круга.
Если точка A лежит вне круга, OA > R, то OA’ < R и, следовательно, точка A переходит в точку внутри круга.
Если точка A при инверсии переходит в точку A’, то точка A’ при этой
же инверсии переходит в точку A.
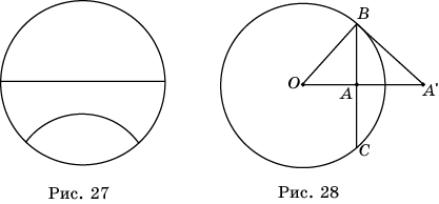
Пусть точка A лежит внутри данного круга с центром в точке O и
радиусом R (рис. 28). Построим точку A’, в которую переходит точка A при
инверсии. Для этого через точку A проведем хорду BC, перпендикулярную OA. Через точку B проведем касательную к окружности. Точка пересечения
этой касательной с лучом OA будет искомой точкой A’. Действительно, треугольники OAB и
OBA’ подобны. Поэтому ![]() Следовательно, OA
Следовательно, OA![]() OA’ = R2.
OA’ = R2.
Инверсию относительно окружности можно
рассматривать как аналог симметрии относительно прямой на плоскости. При
симметрии относительно прямой полуплоскости меняются местами, а при инверсии
относительно окружности меняются местами внутренняя и внешняя область
окружности.
Установим несколько свойств инверсии.
Свойство
1. При инверсии относительно
окружности с центром в точке O точки A, B переходят в точки A’, B’ такие, что треугольники OAB и OB’A’ подобны.
Действительно, в этом случае OA![]() OA’ = R2 = OB
OA’ = R2 = OB![]() OB’ (рис. 29). Следовательно,
OB’ (рис. 29). Следовательно, ![]() Значит, треугольники OAB и
OB’A’ подобны.
Значит, треугольники OAB и
OB’A’ подобны.
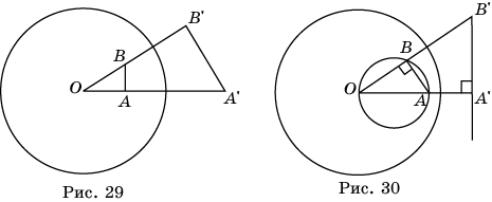
Свойство 2. При инверсии относительно окружности с центром в
точке O окружности, проходящие через точку O (без самой
точки O), переходят в прямые, не проходящие через точку O.
Действительно, пусть OA – диаметр окружности, проходящей через точку O, B – точка, принадлежащая этой окружности (рис. 30). Тогда угол OBA равен 90![]() и равен углу OA’B’.
Следовательно, точка B’ принадлежит прямой, проходящей через точку A’ и
перпендикулярной OA.
и равен углу OA’B’.
Следовательно, точка B’ принадлежит прямой, проходящей через точку A’ и
перпендикулярной OA.
Свойство
3. При инверсии относительно окружности с центром в точке O
окружности, не проходящие через точку O, переходят в окружности, не проходящие через точку O.
Действительно, пусть AB – диаметр
окружности, не проходящей через точку O. Точка C принадлежит этой окружности (рис. 31). Тогда ![]() OCA =
OCA = ![]() OA’C’,
OA’C’, ![]() OCB =
OCB = ![]() OB’C’.
Следовательно,
OB’C’.
Следовательно, ![]() A’C’B’ =
A’C’B’ = ![]() OB’C’ -
OB’C’ - ![]() OA’C’ =
OA’C’ = ![]() OCB -
OCB - ![]() OCA =
OCA = ![]() ACB = 90
ACB = 90![]() . Значит, точка C’ будет
принадлежать окружности с диаметром A’B’.
. Значит, точка C’ будет
принадлежать окружности с диаметром A’B’.
Свойство
4. При инверсии относительно окружности с центром в точке O
окружности, перпендикулярные данной окружности, переходят сами в себя.
Действительно, пусть окружность
пересекает данную окружность в точках A и B и образует с ней прямые углы (рис. 32). Тогда прямые OA и
OB
являются касательными к этой окружности. При инверсии окружность перейдет в
окружность с теми же самыми касательными в точках A и B, т.е. в ту же самую окружность.
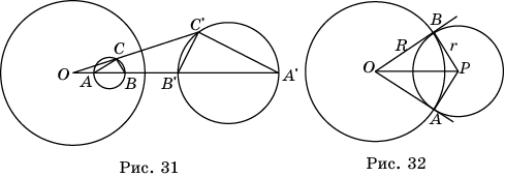
Заметим, что две окружности с центрами O, P и
радиусами R, r перпендикулярны (рис. 32), если углы OAP и
OBP –
прямые. Значит, расстояние OP между центрами перпендикулярных окружностей равно ![]() .
.
Для плоскости Лобачевского будем
называть симметрией инверсию относительно окружности, перпендикулярной
данной. Кроме таких симметрий имеются еще и симметрии относительно прямых,
проходящих через центр данной окружности.
Две фигуры на плоскости Лобачевского называются
равными, если одну из них можно перевести в другую с помощью последовательного
применения одной или нескольких симметрий.
Правильным многоугольником
называется многоугольник, у которого равны все стороны и углы.
В отличие от обычной плоскости, на плоскости
Лобачевского углы правильного n-угольника не равны ![]() , а могут принимать любые значения, большие нуля и меньшие
, а могут принимать любые значения, большие нуля и меньшие ![]() .
.
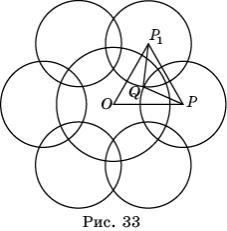
Построим, например, правильный шестиугольник. Пусть
дана окружность с центром O и радиусом R, ограничивающая плоскость Лобачевского. Будем
называть ее окружностью Лобачевского. Проведем какую-нибудь окружность с
центром P и радиусом r, пересекающую данную окружность и такую, что угол AOB больше
60![]() . Будем называть ее производящей окружностью. Поворачивая эту
окружность вокруг центра O на углы, кратные 60
. Будем называть ее производящей окружностью. Поворачивая эту
окружность вокруг центра O на углы, кратные 60![]() , получим шесть окружностей, дуги которых, расположенные
внутри исходной окружности, ограничивают искомый правильный шестиугольник (рис.
33).
, получим шесть окружностей, дуги которых, расположенные
внутри исходной окружности, ограничивают искомый правильный шестиугольник (рис.
33).
Выясним, какие углы имеет этот правильный
шестиугольник. Напомним, что угол между двумя окружностями равен углу между
касательными, проведенными в точке пересечения этих окружностей. Как не трудно
видеть, угол между окружностями с центрами в точках P и P1 равен
углу PQP1 (рис.
33). Имеем, OP = OP1 =![]() , QP = QP1 = r. Так как
угол POP1 равен 60
, QP = QP1 = r. Так как
угол POP1 равен 60![]() , то треугольник POP1 –
равносторонний и, следовательно, PP1 =
, то треугольник POP1 –
равносторонний и, следовательно, PP1 = ![]() . С другой стороны, по
теореме косинусов, PP12 = QP2 + QP12 – 2QP
. С другой стороны, по
теореме косинусов, PP12 = QP2 + QP12 – 2QP![]() QP1cos
QP1cos![]() PQP1 = 2r2 – 2r2cos
PQP1 = 2r2 – 2r2cos![]() PQP1. Из
равенства R2 + r2 = 2r2 – 2r2cos
PQP1. Из
равенства R2 + r2 = 2r2 – 2r2cos![]() PQP1 получаем
PQP1 получаем
![]() .
.
В частности, если R = r, то угол
построенного правильного шестиугольника будет равен 90![]() .
.
Паркетом на плоскости
Лобачевского называется такое ее заполнение многоугольниками, при котором любые
два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не
имеют общих точек.
Паркет называется правильным, если он
состоит из равных правильных многоугольников.
Из сказанного выше следует, что в каждой
вершине правильного паркета на плоскости Лобачевского может сходиться любое
число правильных треугольников, большее шести; любое число правильных
четырехугольников, большее четырех; любое число правильных пятиугольников,
большее трех и т.д.
Таким образом, на плоскости Лобачевского имеется
бесконечно много правильных паркетов из треугольников, четырехугольников,
пятиугольников и т.д.
На рисунке 34 показан паркет из правильных
шестиугольников. В каждой его вершине сходится четыре шестиугольника. Сначала
был нарисован центральный правильный шестиугольник с углами при вершинах 90![]() . Другие правильные шестиугольники искомого паркета были
получены из построенного правильного шестиугольника симметриями плоскости
Лобачевского.Для плоскости Лобачевского будем называть симметрией инверсию
относительно окружности, перпендикулярной данной. Кроме таких симметрий имеются
еще и симметрии относительно прямых, проходящих через центр данной окружности.
. Другие правильные шестиугольники искомого паркета были
получены из построенного правильного шестиугольника симметриями плоскости
Лобачевского.Для плоскости Лобачевского будем называть симметрией инверсию
относительно окружности, перпендикулярной данной. Кроме таких симметрий имеются
еще и симметрии относительно прямых, проходящих через центр данной окружности.
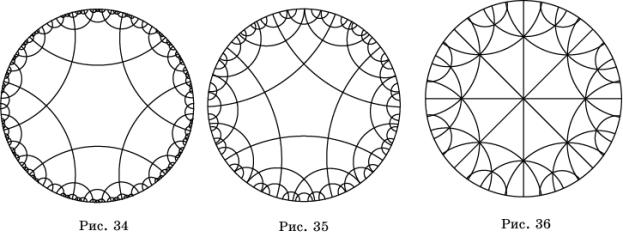
На рисунке 35 показан паркет из правильных пятиугольников.
В каждой его вершине сходится четыре пятиугольника. Сначала был нарисован
центральный правильный пятиугольник с углами при вершинах 90![]() . Остальные пятиугольники были получены из него симметриями
плоскости Лобачевского.
. Остальные пятиугольники были получены из него симметриями
плоскости Лобачевского.
На рисунке 36 показан паркет из правильных
треугольников. В каждой его вершине сходится восемь треугольников с углами при
вершинах 45![]() .
.
Упражнения
1. Выясните, куда при инверсии относительно окружности
с центром в точке O переходят прямые, проходящие через точку O.
2. При инверсии окружность перешла в окружность.
Перешел ли: а) центр окружности в центр окружности; б) диаметр окружности в
диаметр окружности?
3. На каком расстоянии от центра O окружности
радиуса R должен находиться центр P окружности радиуса r, чтобы при инверсии относительно первой окружности
вторая окружность переходила сама в себя?
4. Постройте прямую, проходящую через две данные точки
A и
B на
плоскости Лобачевского (рис. 37).
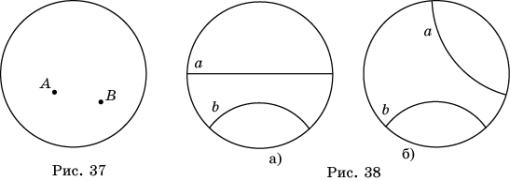
5. Для данных прямых a и b на плоскости Лобачевского (рис. 38 а, б) постройте
прямую b’, симметричную b относительно прямой a.
6. Для данных прямых a и b на плоскости Лобачевского (рис. 38 а, б) укажите
симметрию, переводящую прямую a в прямую b.
7. Для данного отрезка OA на прямой a (рис. 39 а, б) постройте отрезки OB = 2OA, OC = 3OA.
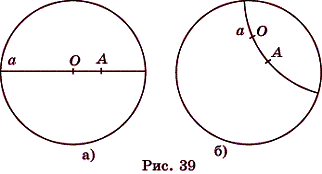
8. Для данных точек O и A на прямой a (рис. 39 а, б) укажите симметрию, переводящую прямую a в
себя и точку O – в точку A.
9. Определите понятие поворота на плоскости Лобачевского.
Докажите, что поворот переводит фигуры на плоскости Лобачевского в равные им
фигуры.
10. Докажите, что симметрия на плоскости Лобачевского
сохраняет углы, т.е. если угол между прямыми a и b равен ![]() , то угол между прямыми a’ и b’, симметричными a и b относительно некоторой прямой c, также
равен
, то угол между прямыми a’ и b’, симметричными a и b относительно некоторой прямой c, также
равен ![]() .
.
11. Какие фигуры образуют окружности на плоскости
Лобачевского?
12. Приведите пример треугольника на плоскости
Лобачевского, около которого нельзя описать окружность.
13. Докажите, что около любого правильного
многоугольника на плоскости Лобачевского можно описать окружность.
14. Объясните, как на плоскости Лобачевского можно
построить правильный треугольник: а) с центром в центре плоскости Лобачевского;
б) в вершиной в центре плоскости Лобачевского.
15. Объясните, как на плоскости Лобачевского можно
построить правильный: а) четырехугольник; б) пятиугольник; в) восьмиугольник с
центром в центре плоскости Лобачевского. Какого радиуса следует взять производящую
окружность, и каким должно быть расстояние от ее центра до центра окружности
Лобачевского, чтобы углы указанных правильных многоугольников были равны 90![]() ?
?
16. Из любого ли треугольника на плоскости
Лобачевского можно составить паркет?
17. В каком случае из правильного треугольника на
плоскости Лобачевского можно составить паркет?
18. Можно ли на плоскости Лобачевского составить
паркет из правильных треугольников, в каждой вершине которого сходится: а)
четыре стороны; б) пять сторон; в) шесть сторон; г) семь сторон?
19. Можно ли составить паркет из треугольников, равных
данному треугольнику с углами 30![]() , 45
, 45![]() , 60
, 60![]() ?
?
20. Составьте паркет из какого-нибудь неправильного
треугольника.
21. Выясните, каким условиям должны удовлетворять углы
треугольника на плоскости Лобачевского, чтобы из него можно было составить
паркет.
22. Можно ли на плоскости Лобачевского составить
паркет из правильных четырехугольников, в каждой вершине которого сходится: а)
четыре стороны; б) пять сторон; в) шесть сторон; г) семь сторон?
23. Составьте паркет из правильных четырехугольников,
в каждой вершине которого сходится восемь сторон.
24. Выясните, каким условиям должны удовлетворять углы
четырехугольника на плоскости Лобачевского, чтобы из него можно было составить
паркет.
25. Составьте паркет из правильных восьмиугольников, в
каждой вершине которого сходится четыре стороны.
26. Определите понятие полуправильного паркета на
плоскости Лобачевского. Приведите пример.
27. Определите понятие двойственного паркета.
Приведите пример.
28. Образуют ли дуги окружностей на рисунке 26
полуправильный паркет на плоскости Лобачевского?
29. Какое наименьшее число красок потребуется для
раскраски паркетов на рисунках 34 – 36 так, чтобы соседние многоугольники были
окрашены в разные цвета?
30. Для окружности на координатной плоскости,
заданной уравнением x2 + y2 = R2, и
точки A(x0, y0),
найдите координаты точки A’,
полученной из точки A инверсией относительно данной
окружности.
31.
Используя координатный метод, докажите, что при инверсии относительно
окружности с центром в точке O(0, 0)
окружности, не проходящие через точку O, переходят в окружности, не проходящие через точку O, а
окружности, проходящие через точку O (без самой точки O), переходят в прямые, не проходящие через точку O.
3. Паркеты на сфере
Напомним, что аналогом многоугольника
на сфере является фигура, ограниченная дугами больших окружностей. Мы будем
называть такие фигуры сферическими многоугольниками, а
соответствующие дуги больших окружностей – сторонами. Легко видеть, что
сферический многоугольник может быть получен как пересечение сферы и
многогранного угла с вершиной в центре этой сферы. Сферический многоугольник
называется правильным, если равны все его стороны и углы.
Паркетом на сфере называется
такое заполнение сферы сферическими многоугольниками, при котором любые два
сферических многоугольника либо имеют общую сторону, либо имеют общую вершину,
либо не имеют общих точек.
Паркет на сфере называется правильным, если он
состоит из равных правильных сферических многоугольников.
Паркет на сфере называется полуправильным, если он
состоит из правильных сферических многоугольников (возможно, с разным числом
сторон) и для любых его вершин существует движение сферы, переводящее паркет
сам в себя и одну из данных вершин в другую.
Отметим связь правильных и полуправильных
паркетов на сфере с правильными и полуправильными многогранниками.
Напомним, что выпуклый многогранник называется правильным,
если его гранями являются равные правильные многоугольники и в каждой вершине
сходится одинаковое число ребер.
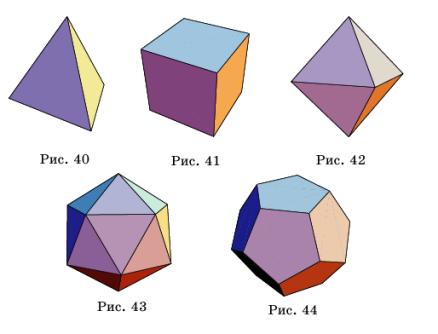
Имеется пять типов правильных многогранников: тетраэдр,
его гранями являются четыре правильных треугольника (рис. 40); гексаэдр
(куб)
– многогранник, гранями которого являются шесть квадратов (рис. 41); октаэдр,
его гранями являются восемь правильных треугольников (рис. 42); икосаэдр,
его гранями являются двадцать правильных треугольников (рис. 43); додекаэдр,
его гранями являются двенадцать правильных пятиугольников (рис. 44).
Полуправильным многогранником
называется выпуклый многогранник, гранями которого являются правильные
многоугольники, возможно, и с разным числом сторон, и для любых двух вершин
существует движение, переводящее многогранник сам в себя и одну из данных
вершин в другую.
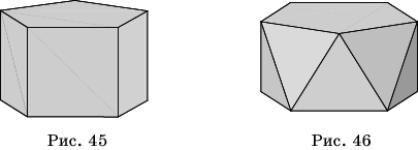
К полуправильным многогранникам относятся
правильные призмы, все ребра которых равны. Например, правильная
шестиугольная призма на рисунке 45 имеет своими гранями два правильных шестиугольника
- основания призмы, и шесть квадратов, образующих боковую поверхность призмы.
К полуправильным многогранникам относятся и, так называемые, антипризмы
с равными ребрами. На рисунке 46 мы видим пятиугольную антипризму, полученную
из пятиугольной призмы поворотом одного из оснований относительно другого на
угол 36![]() . Каждая вершина верхнего и нижнего оснований соединена с
двумя ближайшими вершинами другого основания.
. Каждая вершина верхнего и нижнего оснований соединена с
двумя ближайшими вершинами другого основания.
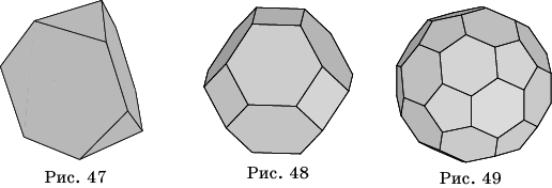
Кроме этих двух бесконечных серий полуправильных
многогранников, имеется еще 13 полуправильных многогранников, которые впервые
открыл и описал Архимед - это тела Архимеда.
Самые простые из них получаются из правильных
многогранников операцией "усечения", состоящей в отсечении
плоскостями углов многогранника. Если срезать углы тетраэдра плоскостями,
каждая из которых отсекает третью часть его ребер, выходящих из одной вершины,
то получим усеченный тетраэдр, имеющий восемь граней (рис. 47). Из них
четыре - правильные шестиугольники, и четыре - правильные треугольники. В
каждой вершине этого многогранника сходятся три грани.
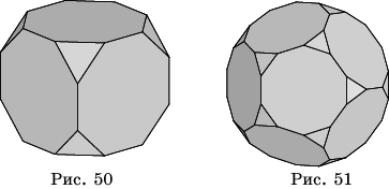
Если указанным образом срезать вершины октаэдра и
икосаэдра, то получим соответственно усеченный октаэдр (рис. 48) и усеченный
икосаэдр (рис. 49). Обратите внимание на то, что поверхность футбольного
мяча изготавливают в форме поверхности усеченного икосаэдра. Из куба и
додекаэдра также можно получить усеченный куб (рис. 50) и усеченный
додекаэдр (рис. 51).
Для того чтобы получить еще один полуправильный
многогранник, проведем в кубе отсекающие плоскости через середины ребер,
выходящих из одной вершины. В результате получим полуправильный многогранник,
который называется кубооктаэдром (рис. 52). Его гранями являются шесть квадратов,
как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его
название - кубооктаэдр.
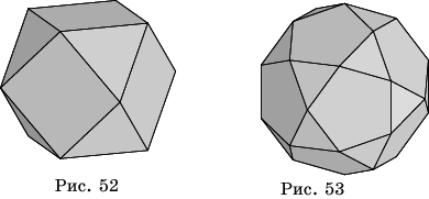
Аналогично, если в додекаэдре отсекающие
плоскости провести через середины ребер, выходящих из одной вершины, то получим
многогранник, который называется икосододекаэдром (рис. 53). У него
двадцать граней - правильные треугольники, и двенадцать граней - правильные
пятиугольники, т.е. все грани икосаэдра и додекаэдра.
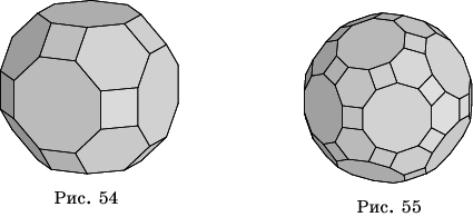
Следующие два многогранника называются усеченный
кубооктаэдр (рис. 54) и усеченный икосододекаэдр (рис. 55).
Однако они не получаются операцией «усечения» из кубооктаэдра и
икосододекаэдра, соответственно. Действительно, если в кубооктаэдре и
икосододекаэдре провести отсекающие плоскости, то в сечениях получатся
прямоугольники, а не квадраты, как требуется.
На рисунке 56 изображен ромбокубооктаэдр. Он
состоит из граней куба и октаэдра, к которым добавлены еще 12 квадратов.
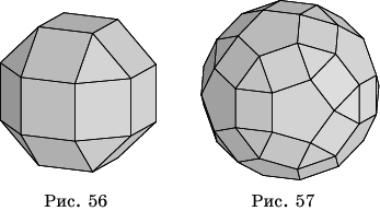
На рисунке 57 изображен ромбоикосододекаэдр,
состоящий из граней икосаэдра, додекаэдра и еще 30 квадратов.
На рисунках 58 и 59 представлены соответственно,
так называемые, плосконосый (иногда называют курносый) куб
и плосконосый
(курносый)
додекаэдр,
которые состоят из граней куба или додекаэдра, окруженных правильными треугольниками.
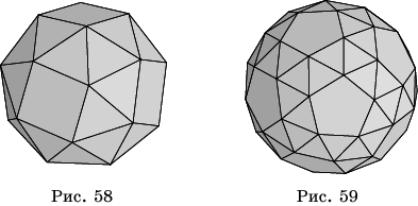
Легко видеть, что каждому паркету на сфере,
состоящему из правильных сферических многоугольников, можно сопоставить
многогранник, вершинами которого будут вершины этого паркета. При этом
правильному паркету на сфере соответствует правильный многогранник, а
полуправильному паркету – полуправильный многогранник. Наоборот, каждому
правильному и полуправильному многограннику можно сопоставить паркет на сфере,
описанной около этого многогранника, вершинами которого будут вершины этого
многогранника. При этом правильному многограннику соответствует правильный
паркет на сфере, а полуправильному многограннику – полуправильный паркет.
Имеется взаимнооднозначное соответствие между
правильными и полуправильными паркетами на сфере и правильными и
полуправильными многогранниками. Таким образом, на сфере имеется пять
правильных паркетов, соответствующих правильным многогранникам; две бесконечные
серии полуправильных паркетов, соответствующих призмам и антипризмам, и 13
полуправильных паркетов, соответствующих телам Архимеда.
Также как и на плоскости, наличие только пяти
типов правильных паркетов на сфере обусловлено не величинами углов правильных
сферических многоугольников, а более общими топологическими свойствами сферы.
Топология – раздел геометрии,
изучающий свойства фигур, не меняющиеся при непрерывных деформациях, включающих
в себя растяжения, сжатия, изгибания и т.п. Две фигуры называются топологически
эквивалентными, если одна из них получается из другой с помощью
непрерывной деформации. Так, например, все n-угольники
топологически эквивалентны, все простые замкнутые линии на плоскости
топологически эквивалентны окружности.
Рассмотрим паркеты на сфере, образованные
криволинейными многоугольниками. Паркет называется топологически правильным,
если он состоит из одноименных многоугольников и в каждой вершине сходится
одинаковое число сторон. Докажем, что существует только пять типов
топологически правильных паркетов на сфере, которые соответствуют правильным
многогранникам. Для этого воспользуемся теоремой Эйлера о числе вершин (В),
ребер (Р) и граней (Г) выпуклого многогранника, переформулированной на язык
паркетов.
Теорема. Для
любого паркета на сфере выполняется следующее равенство:
В – Р + Г = 2,
где В – число вершин, Р – число сторон (ребер), Г – число многоугольников
(граней) данного паркета.
Доказательство. Для данного паркета
рассмотрим какую-нибудь его сторону (ребро), соединяющую две вершины. Стянем ее
вместе с вершинами в одну точку. При этом число вершин уменьшится на единицу
(вместо двух вершин стала одна), число ребер уменьшится на единицу, число
граней не изменится. Следовательно, В – Р + Г при этом не изменится. Будем
последовательно стягивать ребра, соединяющие различные вершины, пока не
останется одна вершина, а стороны превратятся в петли с началом и концом в
данной вершине. При этом В – Р + Г будет таким же, как и у исходного паркета. Уберем
одно из ребер - петель. При этом число вершин не изменится, число ребер
уменьшится на единицу, число граней уменьшится на единицу (две грани соединятся
в одну). Следовательно, В – Р + Г при этом не изменится. Будем последовательно
убирать ребра, пока не останется одно ребро. В результате В – Р + Г будет таким
же, как у исходного паркета. При этом В = 1, Р = 1, Г = 2, т.е. В – Р + Г = 2.
Значит, равенство В – Р + Г = 2 справедливо и для исходного паркета.
Теорема. На
сфере существует только пять типов топологически правильных паркетов.
Доказательство. Пусть
дан топологически правильный паркет на сфере, составленный из n-угольников,
и в каждой вершине сходится m сторон. Ясно, что n и m
больше или равны трем. Обозначим, как и раньше, В - число вершин, Р - число
сторон (ребер) и Г - число многоугольников (граней) этого паркета. Тогда
Г![]() n = 2P; Г =
n = 2P; Г =![]() ; B
; B![]() m = 2P; В =
m = 2P; В = ![]() .
.
По теореме Эйлера В - Р + Г
= 2 и, следовательно,
![]()
Откуда Р = ![]() . Из полученного равенства, в частности, следует, что
должно выполняться неравенство 2n + 2m – nm >
0, которое эквивалентно неравенству (n – 2)(m – 2)
< 4.
. Из полученного равенства, в частности, следует, что
должно выполняться неравенство 2n + 2m – nm >
0, которое эквивалентно неравенству (n – 2)(m – 2)
< 4.
Найдем
всевозможные значения n и m,
удовлетворяющие найденному неравенству, и заполним следующую таблицу.
|
n
m |
3 |
4 |
5 |
|
3 |
B=4, Р=6, Г=4 Тетраэдр |
В=6, Р=12, Г=8 Октаэдр |
В=12,
Р=30, Г=20 Икосаэдр |
|
4 |
В=8, Р=12, Г=4 куб |
Нет |
Нет |
|
5 |
В=20,
Р=30, Г=12 додекаэдр |
Нет |
Нет |
Аналогичным образом можно определить понятие
топологически полуправильного паркета и доказать, что никаких других
топологически правильных паркетов на сфере, кроме перечисленных выше,
соответствующих полуправильным многогранникам, не существует.
Рассмотрим паркеты, двойственные к правильным и
полуправильным паркетам на сфере. Они
соответствуют многогранникам, двойственным к правильным и полуправильным
многогранникам. Плоскости граней двойственного многогранника проходят через
вершины данного правильного или полуправильного многогранника и касаются сферы,
описанной около этого многогранника.
Применение операции двойственности к
правильным многогранникам (правильным паркетам) не дает новых многогранников
(паркетов). Двойственным многогранником к кубу является октаэдр (рис. 60), к
октаэдру – куб (рис. 61), к икосаэдру – додекаэдр (рис. 62), к додекаэдру –
икосаэдр (рис. 63). Тетраэдр двойственен сам себе.
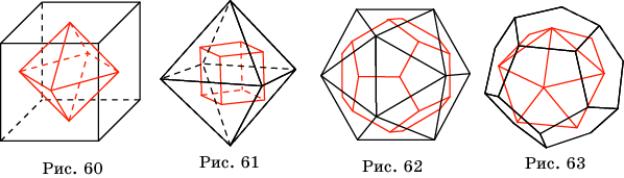
Многогранники, двойственные к полуправильным
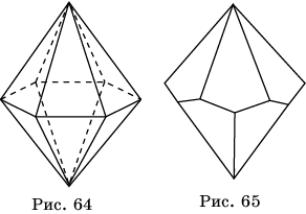
многогранникам, состоят из двух бесконечных серий бипирамид, двойственных
призмам (рис. 64), антибипирамид, двойственных антипризмам (рис. 65), и тринадцати
многогранников
Каталана (рис. 66 – 78), двойственных телам Архимеда.
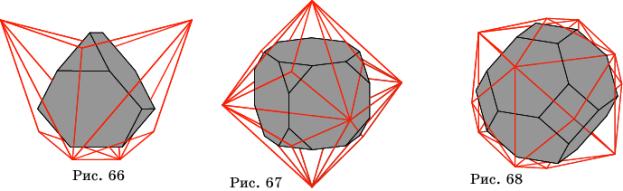
На рисунках 66 – 68 показаны двойственные
многогранники вместе с вписанными в них полуправильными многогранниками.
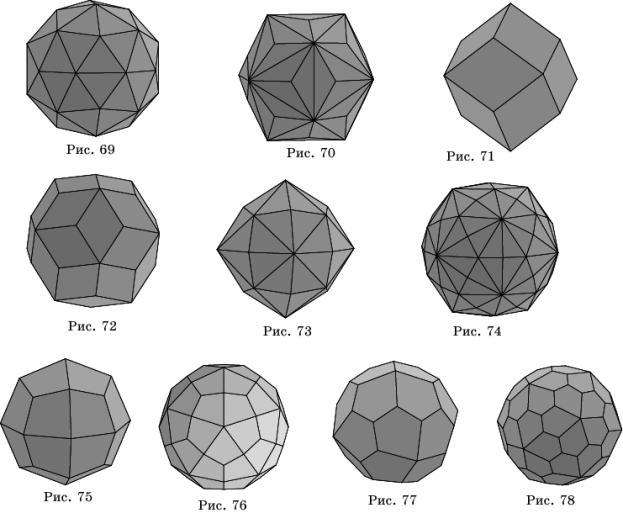
Паркеты на сфере, соответствующие многогранникам,
двойственным к полуправильным многогранникам, состоят из равных (неправильных)
сферических многоугольников. Их вершинами являются центры сферических
многоугольников в исходных полуправильных паркетах.
Упражнения
1. Существует ли паркет на сфере,
состоящий из треугольников, в каждой вершине которого сходится: а) три стороны;
б) четыре стороны; в) пять сторон; г) шесть сторон?
2. Существует ли паркет на сфере,
состоящий из четырехугольников, в каждой вершине которого сходится: а) три
стороны; б) четыре стороны; в) пять сторон; г) шесть сторон?
3. Существует ли паркет на сфере, состоящий
из пятиугольников, в каждой вершине которого сходится: а) три стороны; б)
четыре стороны; в) пять сторон; г) шесть сторон?
4. Существует ли паркет на сфере,
состоящий из шестиугольников, в каждой вершине которого сходится: а) три
стороны; б) четыре стороны; в) пять сторон; г) шесть сторон?
5. Существует ли паркет на сфере,
состоящий из: а) семиугольников; б) восьмиугольников?
6. Может ли паркет на сфере состоять
из: а) двенадцати треугольников; б) пятнадцати треугольников; в) тридцати
треугольников?
7. Можно ли составить паркет на сфере из
греческих крестов (рис. 25), сторонами которых являются дуги больших
окружностей на сфере?
8. В каждой вершине паркета на сфере
сходится четыре стороны. Сколько он имеет вершин, если число его сторон равно
12?
9. Паркет на сфере состоит из
треугольников и шестиугольников. В каждой его вершине сходится три стороны.
Сколько в нем треугольников?
10. Паркет на сфере состоит из
треугольников и четырехугольников. В каждой его вершине сходится три стороны.
Сколько в нем четырехугольников?
11. Паркет на сфере состоит из пятиугольников и
шестиугольников. В каждой его вершине сходится три стороны. Сколько в нем
пятиугольников?
12. Посчитайте, сколько вершин, сторон и
многоугольников в паркетах, соответствующих полуправильным многогранникам,
изображенным на рисунках 47 –59.
13. Посчитайте, сколько вершин, сторон и
многоугольников в паркетах, соответствующих многогранникам, двойственным к
полуправильным многогранникам, изображенным на рисунках 66 – 78.
14. Докажите, что для любого паркета на
сфере выполняются неравенства: 3В ![]() 2Р
2Р ![]() 6В – 12.
6В – 12.
15. Докажите, что для любого паркета на сфере
выполняются неравенства: 3Г ![]() 2Р
2Р ![]() 6Г – 12.
6Г – 12.
16. Докажите, что для любого паркета на
сфере выполняются неравенства: В+4 ![]() 2Г
2Г ![]() 4В – 8.
4В – 8.
17. Докажите, что в любом паркете на сфере или один из
многоугольников – треугольник, или в одной из вершин сходится три стороны.
18. Докажите, что для любого паркета на сфере число
треугольников плюс число вершин, в которых сходится три стороны, больше или
равно восьми.
19. Докажите, что среди многоугольников любого паркета
на сфере найдется треугольник, или четырехугольник, или пятиугольник.
20. Докажите, что для любого паркета на сфере найдется
вершина, в которой сходится три стороны, или четыре стороны, или пять сторон.
21. Какое наименьшее число красок потребуется для раскраски правильных
паркетов на сфере так, чтобы соседние многоугольники были окрашены в разные
цвета?
22. Какое наименьшее число красок потребуется для раскраски
полуправильных паркетов на сфере так, чтобы соседние многоугольники были
окрашены в разные цвета?
4. Паркеты на торе
Тор – поверхность, полученная
вращением окружности относительно прямой, лежащей в плоскости этой окружности и
не имеющей с ней общих точек (рис. 79).
С точки зрения топологии, тор может
быть получен из прямоугольника, склеиванием его противоположных сторон.
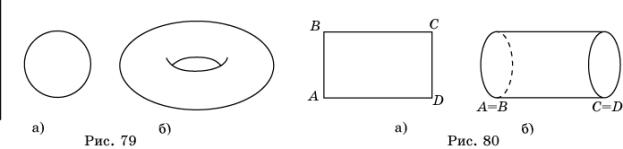
Так, после склеивания сторон BC и
AD прямоугольника
ABCD (рис. 80, а), стороны AB и CD превращаются в окружности, а сам прямоугольник – в
боковую поверхность цилиндра (рис. 80, б). После склеивания оснований этого
цилиндра получаем тор.
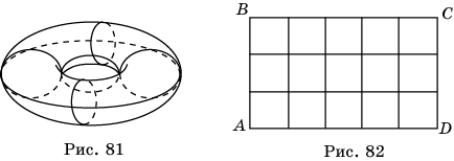
Выясним, какие паркеты могут быть на
торе. Легко видеть, что несколько горизонтальных и вертикальных окружностей на
торе (рис. 81) образуют паркет из четырехугольников, в каждой вершине которого
сходится три стороны. Его можно получить из паркета на плоскости с помощью
операции склеивания. А именно, рассмотрим часть паркета на плоскости,
состоящего из квадратов (рис. 82), заполняющую прямоугольник ABCD. После
склеивания противоположных сторон этого прямоугольника, получим тор вместе с
паркетом из четырехугольников. Аналогичным образом на торе можно получить
паркет из треугольников и шестиугольников, соответствующих правильным паркетам
на плоскости.
Таким образом, на торе имеются, по
крайней мере, три топологически правильных паркета. Выясним, существуют ли
другие топологически правильные паркеты. Для этого воспользуемся следующим
вариантом теоремы Эйлера.
Теорема. Для любого паркета на
торе выполняется следующее равенство:
В – Р
+ Г = 0,
где В – число вершин, Р –
число сторон (ребер), Г – число многоугольников (граней) данного паркета.
Идея доказательства состоит в сведении паркета на торе к
паркету на сфере. Пусть дан паркет на торе. Возьмем какую-нибудь вертикальную
окружность, пересекающую стороны данного паркета в n
точках, и рассмотрим паркет, образованный добавлением этой окружности к данному
паркету. Точки пересечения окружности со сторонами паркета образуют новые
вершины. Их число равно n и, следовательно, число
вершин увеличится на n. Дуги окружности, соединяющие
эти вершины, образуют новые стороны. Их число равно n. Кроме
того, некоторые стороны данного паркета новыми вершинами подразделяются на более мелкие стороны. Всего число сторон в
новом паркете станет на 2n больше, чем в данном. Новые
стороны разбивают многоугольники данного паркета на более мелкие многоугольники.
Так как новых сторон n, то и число многоугольников увеличится на n.
Таким образом, в новом паркете число вершин увеличилось на n,
число сторон – на 2n, и число многоугольников – на
n.
Значит, В – Р + Г не изменилось. Стянем теперь всю добавленную окружность в
точку. Вместо тора получим поверхность, изображенную на рисунке 83, а. Паркет
на торе превратится в паркет на этой поверхности. При этом n вершин
на окружности превратятся в одну, n сторон на окружности исчезнут, а число многоугольников
не изменится. Значит, В – Р + Г увеличится на 1. Разрежем поверхность в точке A.
Получим поверхность, изображенную на рисунке 83, б. При этом, число вершин
увеличится на 1, число сторон и число многоугольников не изменится. Значит, В –
Р + Г увеличится на 1. Поверхность, изображенная на рисунке 83, б,
топологически эквивалентна сфере. Для паркета на этой поверхности имеет место
равенство В – Р + Г = 2. Следовательно, для исходного паркета на торе
выполняется равенство В – Р + Г = 0.
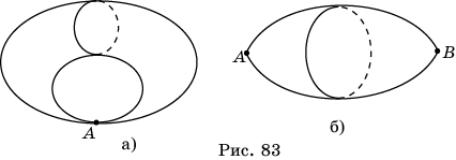
Теорема. На торе существует только пять
типов топологически правильных паркетов:
1) из треугольников, в каждой вершине которых
сходится шесть сторон;
2) из четырехугольников, в каждой вершине которых
сходится четыре стороны;
3) из шестиугольников, в каждой вершине которых
сходится три стороны.
Доказательство. Пусть
дан топологически правильный паркет на торе, составленный из n-угольников,
и в каждой вершине сходится m сторон. Ясно, что n и m
больше или равны трем. Обозначим, как и раньше, В - число вершин, Р - число
сторон (ребер) и Г - число многоугольников (граней) этого паркета. Тогда
Г![]() n = 2P; Г =
n = 2P; Г =![]() ; B
; B![]() m = 2P; В =
m = 2P; В = ![]() .
.
По теореме Эйлера В - Р + Г
= 0 и, следовательно,
![]()
Делая несложные преобразования, получим равенство
(n – 2)(m – 2) = 4. Решая его, находим следующие
пары: n = 3, m = 6; n = 4, m = 4; n = 6, m = 3. Что и завершает
доказательство.
Заметим, что в отличие от плоскости,
где паркеты одного типа топологически эквивалентны, на торе в каждом типе
имеется бесконечно много топологически неэквивалентных паркетов. Например, для
рассмотренного выше паркета из четырехугольников, образованного горизонтальными
и вертикальными окружностями на торе, мы можем увеличивать или уменьшать число
этих окружностей, тем самым увеличивать или уменьшать число четырехугольников,
входящих в паркет. Получаемые при этом паркеты с разным числом
четырехугольников будут топологически не эквивалентны.
Упражнения
1. Существует ли паркет на торе, состоящий из
треугольников, в каждой вершине которого сходится: а) три стороны; б) четыре
стороны; в) пять сторон; г) шесть сторон?
2. Существует ли паркет на торе,
состоящий из четырехугольников, в каждой вершине которого сходится: а) три
стороны; б) четыре стороны; в) пять сторон; г) шесть сторон?
3. Существует ли паркет на торе,
состоящий из пятиугольников, в каждой вершине которого сходится: а) три
стороны; б) четыре стороны; в) пять сторон; г) шесть сторон?
4. Существует ли паркет на торе, состоящий
из шестиугольников, в каждой вершине которого сходится: а) три стороны; б)
четыре стороны; в) пять сторон; г) шесть сторон?
5. Существует ли паркет на торе,
состоящий из: а) семиугольников; б) восьмиугольников?
6. Можно ли составить паркет на торе из греческих
крестов (рис. 25)?
7.
Укажите часть паркета на плоскости,
состоящего из треугольников (рис. 4), заполняющую прямоугольник так, что после
склеивания противоположных сторон этого прямоугольника получается паркет на
торе из треугольников.
8.
Укажите часть паркета на плоскости,
состоящего из шестиугольников (рис. 6), заполняющую прямоугольник так, что
после склеивания противоположных сторон этого прямоугольника получается паркет
на торе из шестиугольников.
9. Для полуправильных
паркетов на плоскости укажите прямоугольники, после склеивания противоположных
сторон которых, получаются топологически полуправильные паркеты на торе.
10. Докажите, что для любого паркета на
торе выполняются неравенства: 3В ![]() 2Р
2Р ![]() 6В.
6В.
11. Докажите, что для любого паркета на торе
выполняются неравенства: 3Г ![]() 2Р
2Р ![]() 6Г.
6Г.
12. Докажите, что для любого паркета на
торе выполняются неравенства: В ![]() 2Г
2Г ![]() 4В.
4В.
13. Докажите, что в любом паркете на торе или один из
многоугольников – треугольник, или в одной из вершин сходится три стороны.
14. Докажите, что в любом паркете на торе или имеется
многоугольник с числом сторон, большим трех, или в одной из вершин сходится
более трех сторон.
15. Верно ли, что для любого паркета на торе число
треугольников плюс число вершин, в которых сходится три стороны, больше или
равно восьми.
16. Докажите, что среди многоугольников любого паркета
на торе найдется треугольник, или четырехугольник, или пятиугольник.
17. Докажите, что для любого паркета на торе найдется
вершина, в которой сходится три стороны, или четыре стороны, или пять сторон.
18. Какое наименьшее число красок потребуется для раскраски топологически
правильных паркетов на торе так, чтобы соседние многоугольники были окрашены в
разные цвета?
19. Кренделем называется поверхность, изображенная на
рисунке 84, а. Она может быть получена из двух торов, если у каждого из них
отрезать небольшой кусок и оставшиеся части склеить по краям (рис. 84, б).
Укажите плоскую фигуру и способ получения кренделя, склеиванием краев этой
фигуры.

20. Установите, чему равно В – Р + Г для паркета на
кренделе.
21. Выясните, какие топологически правильные паркеты
имеются на кренделе.
5. Паркеты в пространстве
По аналогии с паркетом на плоскости, паркетом
в пространстве называется такое заполнение пространства
многогранниками, при котором любые два многогранника либо имеют общую грань,
либо общее ребро, либо общую вершину, либо не имеют общих точек.
Выясним, из каких многогранников можно составить
пространственный паркет. Начнем с правильных многогранников. Ясно, что при
заполнении пространства многогранниками, сумма двугранных углов многогранников,
прилегающих к одному ребру, должна составлять 360![]() . Поэтому из одноименных правильных многогранников
пространственный паркет можно составить только из тех, у которых двугранные
углы имеют вид
. Поэтому из одноименных правильных многогранников
пространственный паркет можно составить только из тех, у которых двугранные
углы имеют вид ![]() ,
, ![]() . Непосредственные вычисления показывают, что единственным
таким многогранником является куб. Из правильных тетраэдров, октаэдров, икосаэдров, додекаэдров пространственных
паркетов составить нельзя.
. Непосредственные вычисления показывают, что единственным
таким многогранником является куб. Из правильных тетраэдров, октаэдров, икосаэдров, додекаэдров пространственных
паркетов составить нельзя.
Перейдем к полуправильным многогранникам. Ясно, что из
правильных треугольных и шестиугольных призм можно составить пространственные
паркеты.
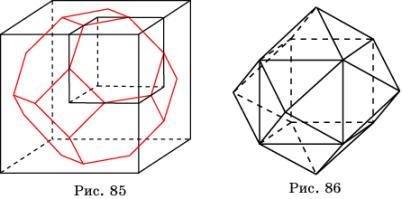
Рассмотрим усеченный октаэдр (рис. 48). Покажем, что
из усеченного октаэдра можно составить пространственный паркет.
Разрежем усеченный октаэдр на восемь равных частей
плоскостями, проходящими через пары противоположных ребер октаэдра (рис. 85).
Каждая такая часть представляет собой половинку куба, полученную разрезанием
куба по плоскости, дающей в сечении куба правильный шестиугольник.
Если взять два равных усеченных октаэдра, один из них
разрезать на восемь равных частей и присоединить эти части к шестиугольным
граням неразрезанного усеченного октаэдра, то получим куб.
Рассмотрим пространственный паркет, состоящий из
кубов, с вписанными в них усеченными октаэдрами. Усеченные октаэдры не
заполняют все пространство. Между ними остаются пустоты. Однако эти пустоты
расположены вокруг вершин кубов и представляют собой объединение восьмых частей
усеченных октаэдров и, следовательно, сами являются усеченными октаэдрами.
Таким образом, все пространство оказывается разбитым на усеченные октаэдры, и
любые два таких усеченных октаэдра получаются друг из друга параллельным
переносом.
Рассмотрим ромбододекаэдр (рис. 71) –
многогранник, двойственный кубооктаэдру, поверхность которого состоит из
двенадцати равных ромбов.
Форму ромбододекаэдра имеет кристалл граната. Поэтому
его называют также гранатоэдр.
Ромбододекаэдр можно получить из двух кубов следующим
образом. Разрежем один из кубов на шесть равных правильных четырехугольных
пирамид с вершинами в центре куба, основаниями которых являются грани куба.
Поставим каждую такую пирамиду основанием на грань неразрезанного куба. Получим
ромбододекаэдр (рис. 86).
Приступим теперь к составлению паркета. Рассмотрим
пространственный паркет из кубов, раскрашенных в черный и белый цвета в
шахматном порядке так, что по граням соприкасаются только черные и белые кубы.
Разобьем белые кубы на правильные четырехугольные пирамиды и присоединим их к
прилегающим черным кубам. В результате получим пространственный паркет из
ромбододекаэдров, причем любые два ромбододекаэдра получаются друг из друга
параллельным переносом.
Приведем пример еще одного многогранника, из которого
можно составить пространственный паркет.
Разрежем ромбододекаэдр плоскостью, проходящей через
центр вписанного в него куба, параллельно одной из граней куба. В сечении будет
квадрат ABCD со стороной, равной диагонали грани куба (рис. 87).
Вставим между двумя половинками ромбододекаэдра правильную четырехугольную
призму. Получим искомый многогранник (рис. 88), поверхность которого состоит из
двенадцати граней: восьми ромбов и четырех шестиугольников.
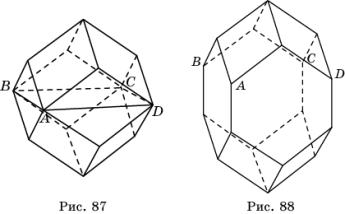
Покажем, что из таких двенадцатигранников можно
составить пространственный паркет. Для этого разрежем паркет из
ромбододекаэдров плоскостями, проходящими через центры черных кубов и
параллельными одной выбранной грани черного куба. В пересечении каждой такой
плоскости с ромбододекаэдрами образуется плоский паркет из квадратов. В каждый
разрез вставим правильные четырехугольные призмы, основаниями которых являются
квадраты из плоского паркета. В результате получим требуемый пространственный
паркет, причем любые два многогранника из этого паркета получаются друг из
друга параллельным переносом.
Заметим, что в пяти, из рассмотренных выше пространственных
паркетов, многогранники расположены параллельно друг другу. Это паркеты из
шестиугольных призм, кубов (параллелепипедов), усеченных икосаэдров,
ромбододекаэдров и двенадцатигранников, полученных из ромбододекаэдра.
Такие выпуклые многогранники, из которых можно
составить пространственный паркет так, чтобы любые два многогранника из этого
паркета получались друг из друга параллельным переносом, называются параллелоэдрами.
Отечественным математиком и кристаллографом Е.С. Федоровым (1853 – 1919) было доказано,
что существует только пять типов параллелоэдров: куб (параллелепипед),
правильная шестиугольная призма, усеченный октаэдр, ромбододекаэдр и
двенадцатигранник, полученный из ромбододекаэдра.
Упражнения
1. Можно ли составить пространственный паркет из
произвольного параллелепипеда?
2. Можно ли составить пространственный паркет из
произвольной: а) треугольной призмы; б) четырехугольной призмы; в)
шестиугольной призмы?
3. Можно ли составить паркет из какой-нибудь
пятиугольной призмы?
4. Найдите двугранные углы: а) правильного тетраэдра;
б) октаэдра; в) икосаэдра; г) додекаэдра и покажите, что из них нельзя
составить пространственный паркет.
5. Найдите двугранные углы, образованные гранями: а)
усеченного октаэдра; б) ромбододекаэдра.
6. Вершинами какого многогранника являются центры
граней ромбододекаэдра?
7. Покажите, что из равных правильных четырехугольных
пирамид можно составить пространственный паркет. Какую нужно выбрать высоту
этой пирамиды, если сторона ее основания равна 1? Найдите двугранные углы этой
пирамиды.
8. Покажите, что из равных правильных четырехугольных
и шестиугольных пирамид можно составить пространственный паркет.
9. Приведите пример неправильной пирамиды, из которой
можно составить пространственный паркет. Найдите ее двугранные углы.
10. Приведите пример тетраэдра (треугольной пирамиды),
из которого можно составить пространственный паркет. Найдите его двугранные
углы.
11. Приведите пример треугольной призмы, которую можно
разбить на три равных тетраэдра.
12. Найдите ребра тетраэдра, поверхность которого
состоит из равных равнобедренных треугольников, из которого можно составить
пространственный паркет.
13. Покажите, что полосу в пространстве, ограниченную
двумя параллельными плоскостями, можно заполнить паркетом из равных тетраэдров.
Найдите ребра этих тетраэдров, если расстояние между параллельными плоскостями
(ширина полосы) равна h.
14. Можно ли составить пространственный паркет из
равных правильных четырехугольных бипирамид?
15. Можно ли составить пространственный паркет из пространственного
креста – многогранника, полученного объединением семи кубов (рис. 89).
16. Покажите, как можно составить пространственный
паркет из усеченных кубов и октаэдров.
17. Покажите, как можно составить пространственный
паркет из кубооктаэдров и октаэдров.
18. Можно ли составить пространственный паркет из
октаэдров и правильных тетраэдров?
19. Какие
многогранники нужно добавить к: а) усеченному кубооктаэдру; б)
ромбокубооктаэдру, чтобы из них можно было составить пространственный паркет?
20. На рисунке
90 изображен многогранник, называемый звездчатым октаэдром, получающийся
продолжением граней октаэдра. Он был открыт Леонардо да
Винчи, затем спустя почти сто лет переоткрыт И. Кеплером и назван им "Stella
octangula" - звезда восьмиугольная. Какой правильный многогранник нужно добавить к нему, чтобы из них
можно было составить пространственный паркет?
21. Какое
наименьшее число красок потребуется для раскраски пространственного паркета из:
а) кубов; б) ромбододекаэдров, при которой многогранники, имеющие общую грань,
окрашиваются в разные цвета?
22. Двойственным
к пространственному паркету, состоящему из многогранников, имеющих центр
симметрии, называется пространственный паркет из многогранников, вершинами
которых являются центры многогранников данного паркета. Какие пространственные
паркеты двойственны паркету из: а) кубов; б) правильных треугольных призм; в)
правильных шестиугольных призм?
23. Найдите
пространственные паркеты двойственные паркетам из: а) усеченных октаэдров; б)
ромбододекаэдров; в) двенадцатигранников, полученных из ромбододекаэдров?
24. Сформулируйте свойство паркетов, двойственных
паркетам из параллелоэдров.
25. Сформулируйте определение топологически правильного
паркета в пространстве. Выясните, существуют ли топологически правильные
паркеты в пространстве, кроме паркета из кубов.
26. Рассмотрим 3-х мерную сферу. В 4-х мерном
пространстве с координатами (x, y, z, t) 3-х мерная сфера с центром в начале координат и
радиусом R задается уравнением x2 + y2 + z2 + t2 = R2. По
аналогии с двумерной сферой, которую (как топологическое пространство) можно
получить из круга, стягиванием в точку его граничной окружности, 3-х мерную
сферу (как топологическое пространство) можно получить из шара, стягиванием в
точку его граничной сферы.
Определите понятие паркета на 3-х мерной сфере.
Найдите, чему равно В – Р + Г – М, где В – число вершин, Р – число ребер, Г –
число граней, М – число многогранников, входящих в паркет.
Определите понятие правильного (топологически
правильного) паркета на 3-х мерной сфере и правильного (топологически
правильного) 4-х мерного многогранника. Установите связь между ними.
Выясните, какие имеются: а) правильные паркеты на 3-х
мерной сфере; б) правильные 4-х мерные многогранники.
27. По аналогии с плоскостью Лобачевского определите
пространство Лобачевского. Что в этом пространстве является: а) точками; б)
прямыми; в) плоскостями? Как определяется равенство фигур?
28. Укажите какой-нибудь паркет в пространстве
Лобачевского.
ЛИТЕРАТУРА
1. Болтянский В.Г. Паркеты из правильных четырехугольников // Квант. – 1989. – № 11. – С. 57.
2. Бончковский Р.Н. Заполнение пространства тетраэдрами // Математическое просвещение. – 1935. – № 4. – С. 26.
2. Делоне Б.,
Житомирский О. Задачник по геометрии. – М. – Л.: Гос. изд. техн.-теорет. литературы,
1950.
3. Колмогоров А.Н. Паркеты из правильных многоугольников // Квант. – 1986. – № 8. – С. 3.
4. Михайлов О. Одиннадцать правильных паркетов // Квант. – 1979. – № 2. – С. 9.
5. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
6. Смирнова
И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе “Paint” // Математика в
школе. – 2000. – № 8. – С. 54.
7. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов
общеобразовательных учреждений. – М.: Мнемозина, 2005.